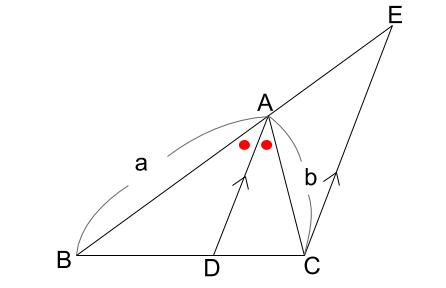
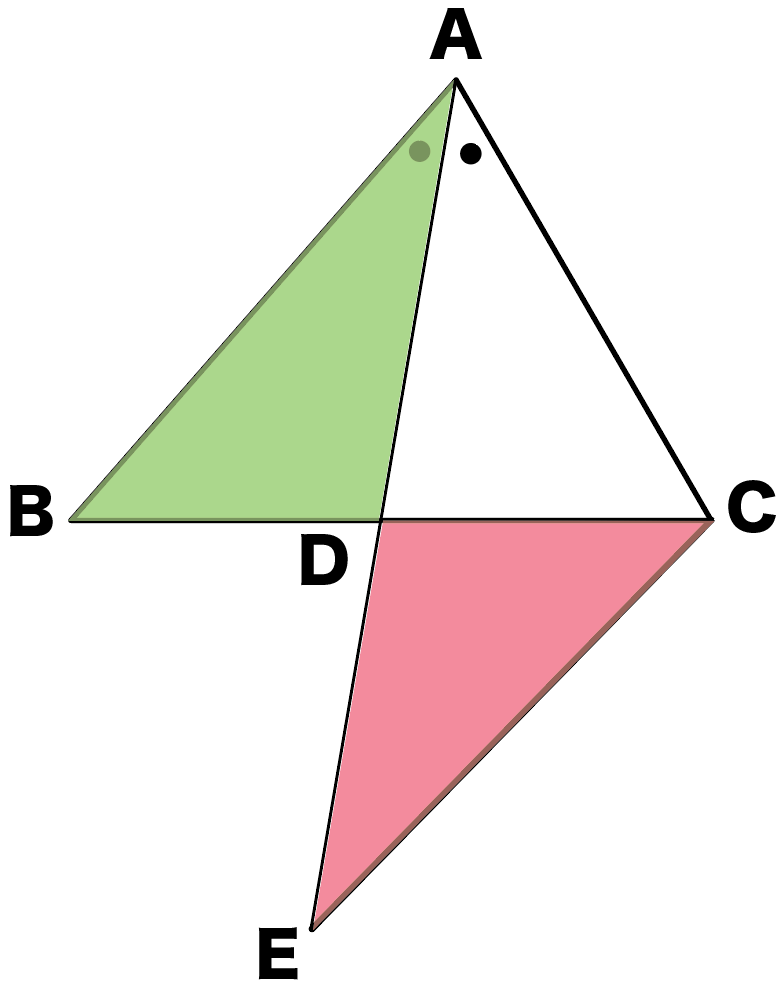
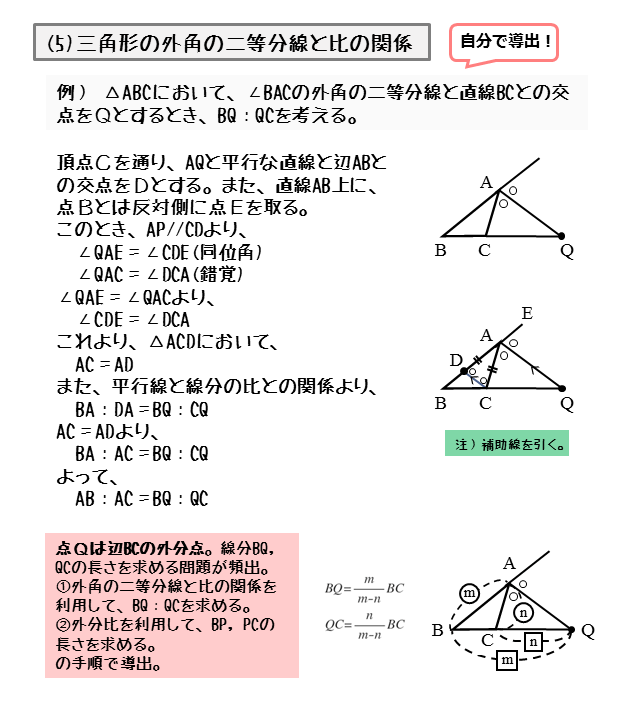
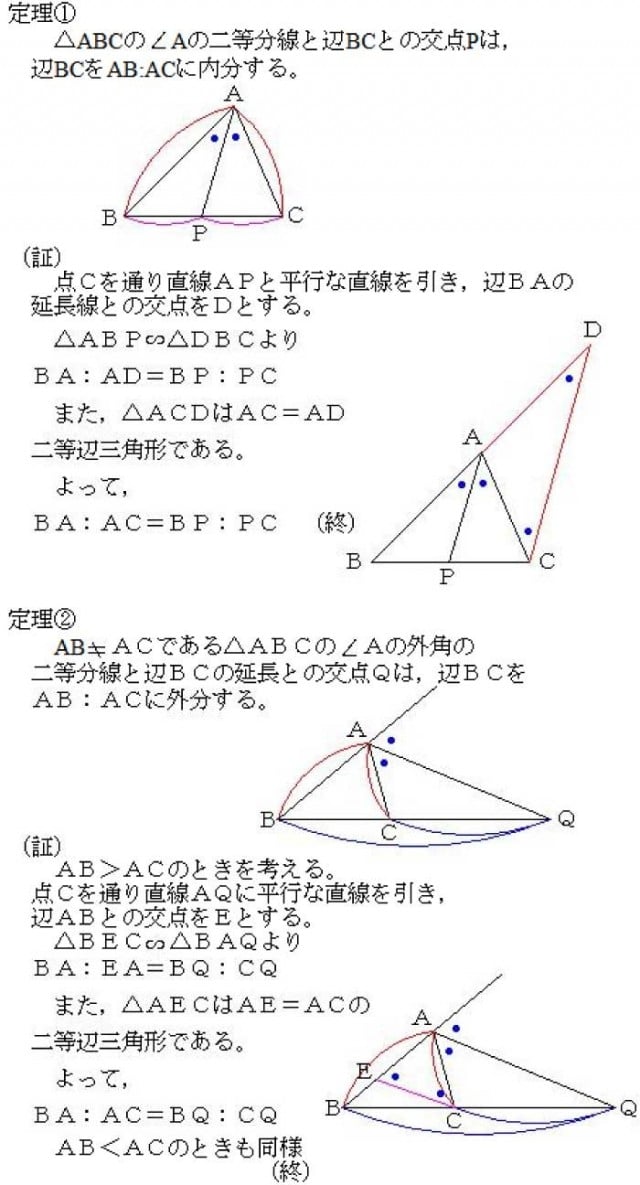
角の2等分線の定理 定理 BD:DC=AB:AC が成り立つ。 証明 点Cを通り、ABに平行な直線と、ADの交点をEとします。 このとき、 より、 となり、 ACEは、AC=CE の二等辺三角形となります。 三角形のひとつの角の二等分線が与えられたとき,次の基本的な比の関係式が成り立ちます. 三角形の内角の二等分線と比: △ ABC △ A B C の ∠A ∠ A の内角の二等分線と辺 BC B C との交点を D D とする.このとき,次の関係式が成り立つ. 三角形の内角・外角の二等分線と辺の比の関係とその証明 三角形の角の二等分線と辺の比Aの二等分線と辺BCの交点P}}は,\ 辺BCを\ \syoumei\ \ 直線APに平行な直線を点Cを通るように引き,\ 直線ABの交点をDとする (右図) (同位角), (錯角)}$ \\ 2zh \phantom { (1)}\ \ 仮定
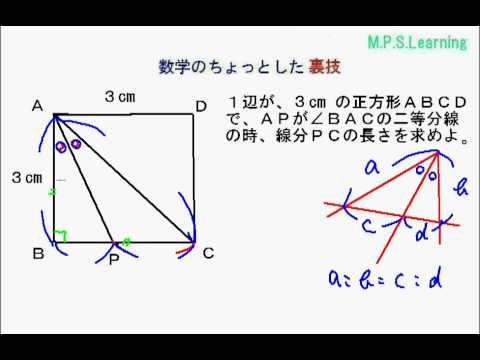
中3数学 角の二等分線と線分比 2 Youtube
二等分線 辺の比
二等分線 辺の比-(三角形の角の二等分線に関する公式2) (証明) CからADに平行な直線を引き、Abとの交点をEとする。 よって、 ACEは二等辺三角形、AE=AC。 ADとECが平行より、AB:AE=BD:DC、 AE=ACだから、AB:AC=BD:DC。相似比は2:3だと分かります。 つまり、他の辺の比も2:3になるので ae:de=be:ce=2:3 とわかります。 このae:de=2:3ということを利用して 次は、 adbと edfに注目すると



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学
∠acb の二等分線を引き, ∠acb の二等分線と円 o の交点のうち,点 c 以外の交点を d とし,線分 cd と線分 ab の交点を e とする。また,線分 ac を点 c の方向へ延長し,その延長線上に cd//fb となるように点 f をとる。このとき,次の(1)・(2)の問いに答えなさい。Page 1 高校で教えたい幾何の問題 角の二等分線の性質を狩る 札幌旭丘高校 中村文則 はじめに 三角形ABC の頂角Aの二等分線を,正確に引けない生徒が意外と多いことに驚く. 辺BC の中点と交わり、なぜか中線になってしまう.「角の二等分」から「辺の二等分」へと安易に結び角の二等分線の作図方法が理解できる。 展 開 40 分 ①角の二等分線に平行な補助線CEを加えた図を示し,平行線と比の関係を用いて課題を解決することを説明する。 ・比の関係が等しい組はどれか考える。 BA:AEとBD:DC
証明・問題の解き方の解説 5月 11, 管理人 数学FUN 中学校の図形の問題において、相似に関連して、いくつか定理を習います。 「平行線と線分の比の定理」や「角の二等分線と辺の比」そして今回解説する「中点連結定理」などです。 定理の使いこの3本の垂直二等分線は、 rqpの外心で交わる。すなわち abcの各頂点から対辺に引いた3本の垂線 ad,be,cf は一点で交わる。 三角形の角の二等分線と辺の比 三角形の角の二等分線に関して、次のこ こんにちは、ウチダです。 今日は、中学1年生及び中学3年生で習う 「角の二等分線」 について、まずは作図方法(書き方)とそれが正しいことの証明を学び、次に角の二等分線と辺の比の定理(性質)を学びます。 また、記事の後半では、外角に関する問題も考察していきたいと思います。 角の二
内角の2等分線と線分の比 解説 次の図のように, abcの∠aの二等分線と対辺bcとの交点をpとします。 という関係が導き出され,角の2等分線と対辺の交点は,その角をはさむ2辺の比に対辺を分割した点になります。問題番号問いの二等分線と辺BCとの交点をDとするときBDの長さを求めなさい,。 15 正解 6 誤 答 例 つまずき原 因 分析と解消 1 無解答 角の二等分線と線分の比について理解してい39ページ ない。角の二等分線に関する公式 ae=bd ae = bd (ab)f=2ab\cos \dfrac {A} {2} (a b)f = 2abcos 2A f^2=abde f 2 = ab− de




三角形の二等分2パターン 角の二等分 中線定理 数学の偏差値を上げて合格を目指す




角の二等分線の長さを導出する4通りの方法 理系のための備忘録
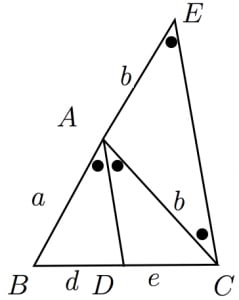
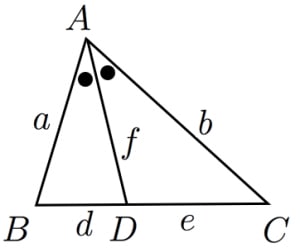
数学35章図形と相似「平行線と線分の比」<準備問題> 組 番 名前 1平行四辺形の定義を書きなさい。 2四角形が平行四辺形であるための条件が3つ書いてあります。あと2つ,条件を書きなさい。 ・2組の向かい合う辺がそれぞれ平行である。 角の二等分線に関する重要な3つの公式 三角形 A B C ABC A BC において, ∠ A \angle A ∠ A の二等分線と辺 B C BC BC の交点を D D D とおく。 A B = a, A C = b, B D = d, AB=a, AC=b, BD=d, A B = a, A C = b, B D = d, D C = e, A D = f DC=e, AD=f D C = e, A D = f とおくとき以下の公式図3のような緑の三角形を考える。 \( \angle A\)の二等分線とその二等分線が辺BCと交わる点Pとする。 定理1を証明するためには、 AB AC = BP PC を証明すれば良い。 線分APに平行でCを通る補助線を下記、その補助線と辺ABとの交点をDとする。



中3数学 角の二等分線定理のポイントと練習問題



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学
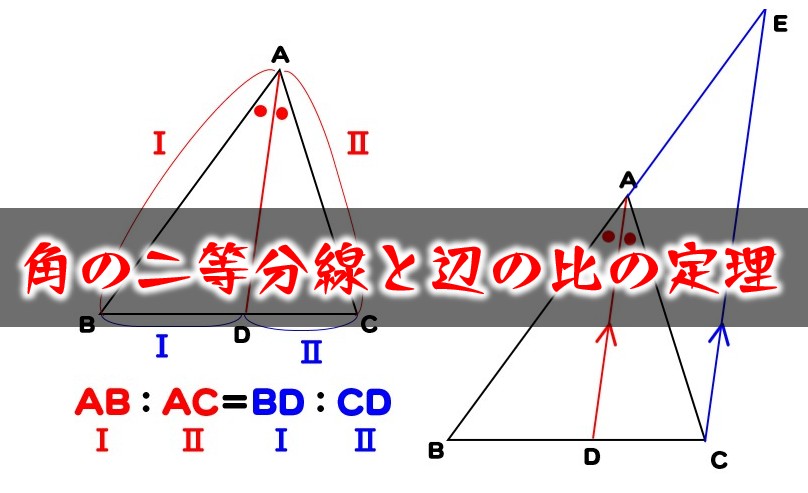
では、なぜ内角の二等分線と比にはこのような性質があるのか証明してみましょう。 まず、辺 と平行な線を点 を通るように引きます。 すると、図のように同位角、錯角により が二等辺三角形になることが分かります、 つまり、 となります。 最後に三角形の角の二等分線に関して,次の定理が成り立つ. ¶ ‡三角形の角の二等分線と比 定理3 4ABCの\Aの二等分線と辺BCと の交点は,辺BCをAB ACに内分する. µ c b c b A B C この定理を証明するために,平行線に関する次の性質を確認しておく.三角形の角の二等分線と辺の比 三角形ABCにおいて、∠BACを二等分する線とBCとの交点をDとしたとき、次の定理が成り立つ。 このテキストでは、この定理を証明します。 証明 図のように、∠BACの二等分線と辺BCとの交点をDと




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su
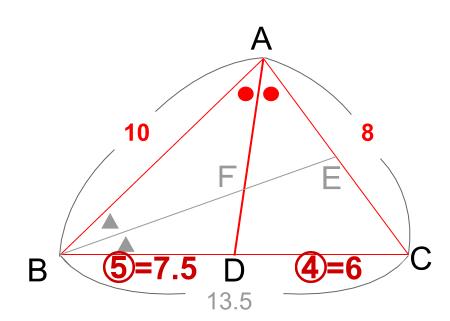
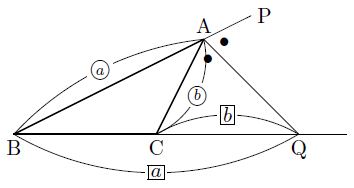
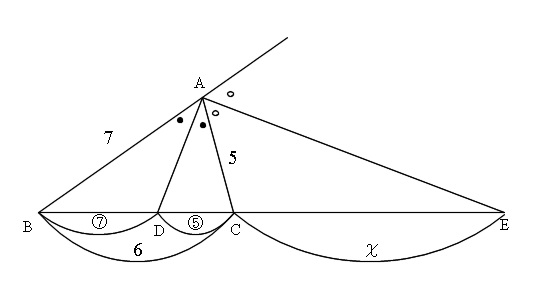
内角の二等分線と辺の比中3数学 問題をノーヒントでやってみよう 略解をチェックしよう 攻略ポイントを確認しよう ・内角の二等分線のある三角形の、等しい辺の比を、それぞれの形で見極めよう。 ・それが言える理由は、平行線と線分の比と3 角の二等分線と比 ab=6,bc=5,ca=4である abcにおいて, ∠aの二等分線と辺bcとの交点をdとし,∠a の外角の二等分線と辺bcの延長との交点をeと する。 次の線分の長さを求めよ。 (1) dc (2) ce b 5 c a d e 6 4 pq b c a p q q b c p a 要点 point内角の二等分線と辺の比の関係 から、 bp:pc=ab:ac が言えるね。つまり、 bp:pc=3:5 だよ。bpはbcを 8個に分けた3個分 と考えることができるから、 bp=(3/8)×bc で答えを出すことができるね。




勉強しよう数学 角の二等分線の長さ 相似図形による定理の証明




苦手を克服 数学aの平面図形で使う定理の一覧 数学a By となりがトトロ マナペディア
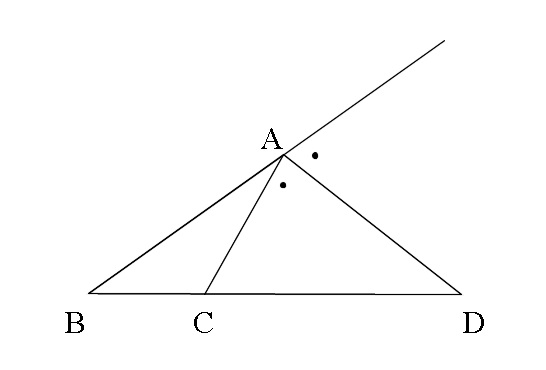
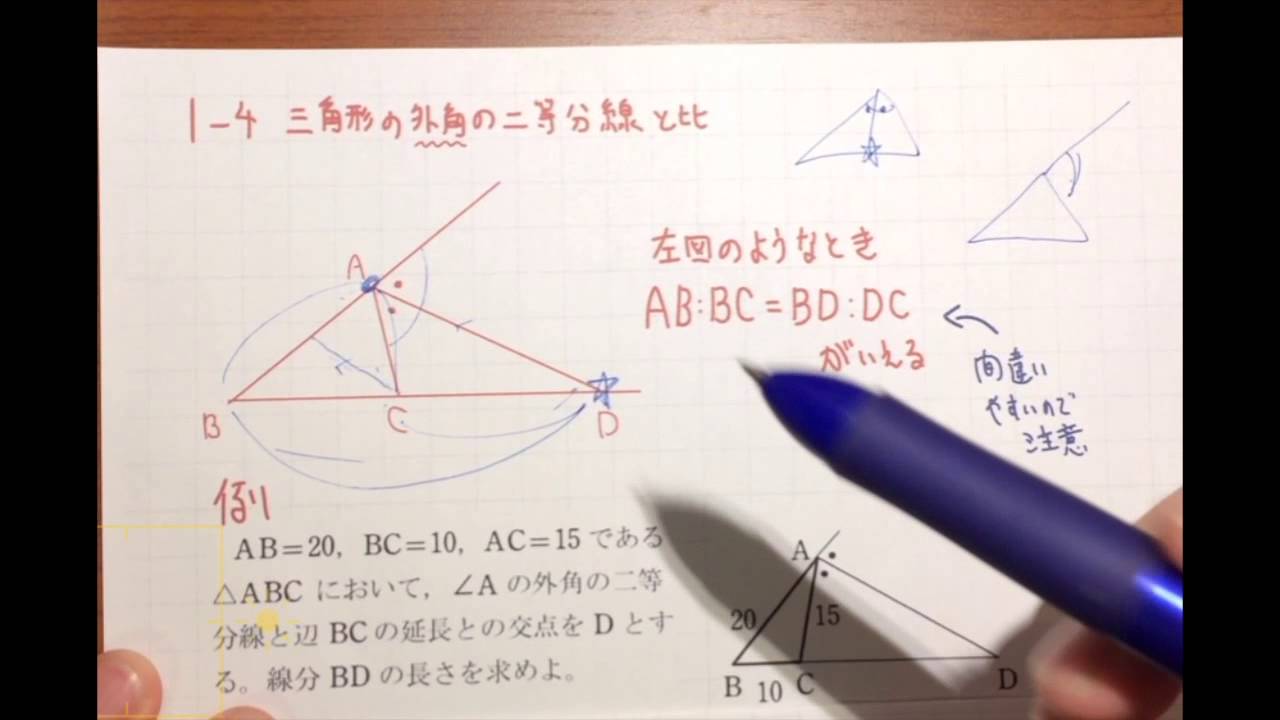
三角形の外角の二等分線と比 $ において,3辺の垂直二等分線が交わる点を $\mathrm{O}$ とすると,上の証明により,点 $\mathrm{O}$ は $\triangle{\mathrm{ABC}}$ の3つの頂点から等距離にある.よって,この点 $\mathrm{O}$ を中心とする半径 $\mathrm{OA}$ の円は, $\triangle知っておくと役に立つ以下の定理があります。 角の 2 2 等分と線分の比 下図のように、角 A A の 2 2 等分線と、 BC B C の交点を D D とします。 このとき、 BD DC = AB AC B D D C = A B A C 一応、中学数学の範囲外なので、頻繁に出題されるものではありませんが 今回の問題は「 角の二等分線と比 」です。 問題 次の図で、 で の内角の二等分線と直線 との交点を 、 の外角の二等分線と直線 との交点を とするとき、 の長さを求めよ。 次のページ「解法のPointと問題解説」 次へ 1 2 中点連結定理と平行線と比



内角の2等分線と線分の比 まなびの学園




角の二等分線と比 おいしい数学
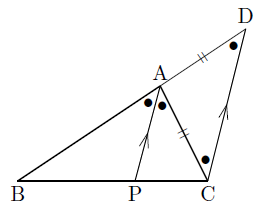
この頁では,角の二等分線を題材にして,補助線の引き方を練習します. 図1 角の二等分線の性質 ABC において右図2のように線分 AD が∠ A を二等分しているとき, BDDC=BAAC が成り立ちます. ※この定理は中学校では習いませんので,中学生に対し 角の二等分線とは、その名の通り、 ある角を二等分した線 のことです。 角を 内分 する「内角の二等分線」と、 外分 する「外角の二等分線」の 種類があります。 内角でも外角でも、 辺の比 は同じ関係式で表されます( 角の二等分線の定理 )。内角の二等分線と辺の比の関係 から、 bp:pc=ab:ac が言えるね。つまり、 bp:3=8:6 だよ。この比例式より、 bp=4 と答えを出すことができるね。よって、辺bcの長さは、 bc=bppc=7 となる



角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学
角の2等分線 三角形の内角の二等分線の長さを求めるの外接円を用いたが,外接円の直径を求めるには次の図が便利である. 三角形の高さAH=hを求めるのはBH=xとおいて簡単に求められる.これは3辺を与えた三角形の面積を求めるときに用いる 中学生によって、直線apは∠aの二等分線である。 (証明 おわり) この点 p を 傍心(ぼうしん)という。 三角形の角の2等分線と辺の比 三角形の角の2等分線に関して、次のことが成り立つ。 "内角の二等分線と比"の公式とその証明です! 内角の二等分線と比公式内角の二等分線と比 ∠aの二等分線とbcの交点をpとすると \(bp:pc=ab:ac\)証明①三角形の相似による証明証明 cを通りapに平行な線とabの延長との交点




三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア




角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su
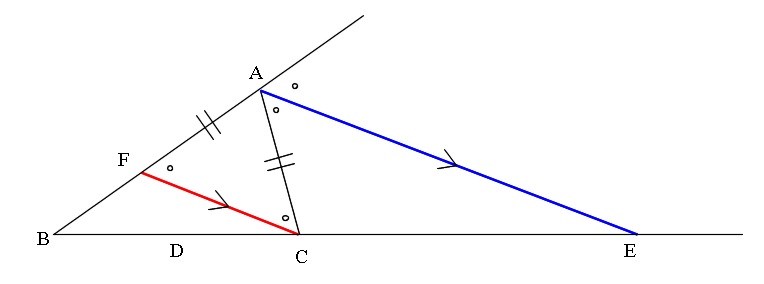
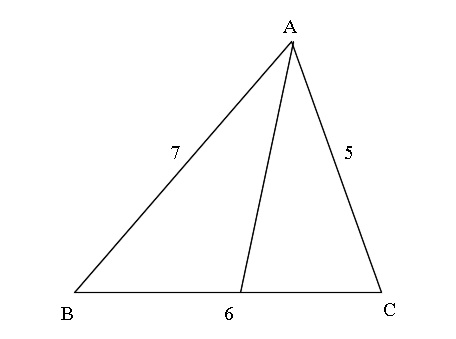
∠bacの二等分線と辺bcの交点をdとする。次の問いに答えよ。 ab=4,ac=10,bc=7のとき bdを求めよ。 a b c d ac=9,bd=3,dc=4 のときabを三角形の二辺の和と、残りの一辺の大小関係について。 辺に関する大小関係 PDF 6113三角形の角の二等分線と線分の比 三角形の角(内角・外角)の二等分線と辺の比について。 三角三角形の外角の二等分線と比の解答 CD = x とおくと、外角の二等分線の定理より、 AB AC = BD DC 7 5 = ( 6 x) x 7 x = 5 ( 6 x) 2 x = 30 x = 15 ∴ CD = 15 二等辺三角形を分割する線の長さ




高校数学a 外角の二等分線と比 例題編 映像授業のtry It トライイット



三角形の内角の二等分線 メネラウスの定理 チェバの定理
角の二等分線と辺の比1 ∠BACの二等分線と辺BCの交点をDとする。 それぞれのxの値を求めよ。 ∠BACの二等分線と辺BCの交点をDとする。 それぞれのxの値を求めよ。この章では,三角形の内角の二等分線,外角の二等分線の性質から始め複比そして射影幾何を学びます. まず,三角形の内角の二等分線,外角の二等分線の性質からはじめましょう. 命題1 abcの∠aの二等分線と辺bcとの交点をpとすれば ab:ac=bp:pc 三角比と角の二等分線 角の二等分線とは、角を同じ大きさに分ける線のことです。下の図で言うと、 AD が $\angle \mathrm{ A }$ の二等分線です。 有名な性質として、 $\mathrm{ AB }\mathrm{ AC }=\mathrm{ BD }\mathrm{ CD }$ になる、というものがあります。 次のように、 C を通り、 AD に平行な線をひくと



1




角の二等分線の長さ の公式の証明 怜悧玲瓏 高校数学を天空から俯瞰する



内角の二等分線と外角の二等分線の定理の覚え方と使い方




中3数学 角の二等分線と線分比 2 Youtube




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学



角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su




高校 数学aの問題です 外角の二等分線の式がどうしてこうなるのかわかりません Clear



外角の2等分線と線分の比 まなびの学園



角の二等分線に関する重要な3つの公式 高校数学の美しい物語



三角形の角の二等分線の性質 定理の証明がわかる5ステップ Qikeru 学びを楽しくわかりやすく




苦手を克服 数学aの平面図形で使う定理の一覧 数学a By となりがトトロ マナペディア




頂角の二等分線は底辺を二等分する Youtube



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




角の2等分線の定理 数学i フリー教材開発コミュニティ Ftext




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学




図形の性質 角の二等分線と比について 日々是鍛錬 ひびこれたんれん



1




内角の二等分線 外角の二等分線の比の定理 証明 Youtube




サクッと解説 角の二等分線と比の特徴となぜ について 数スタ




角の2等分線の定理 数学i フリー教材開発コミュニティ Ftext




角の2等分線によって分ける比 身勝手な主張




二等辺三角形の性質の証明 頂角の二等分線 Youtube




角の二等分線が図で誰でも一発でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学
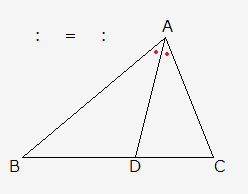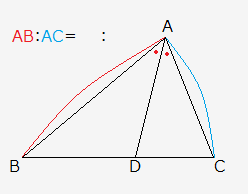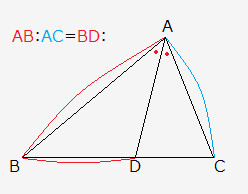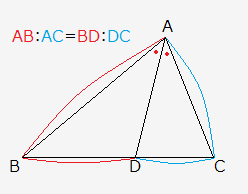



例題で学ぶ高校数学 内角の二等分線の性質



角の二等分線の長さを求める公式 ほのぼの数学頑張ろう



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典
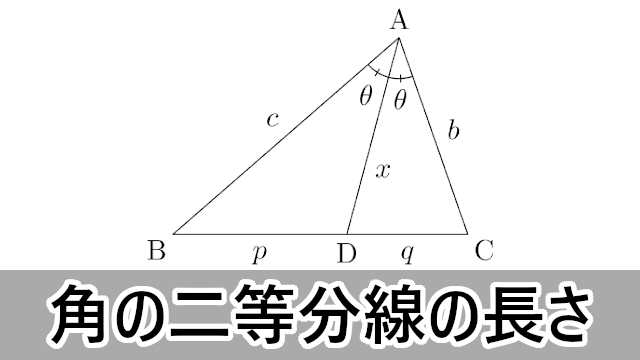



数学ia 三角形の内角の二等分線の長さ 大学入試数学の考え方と解法




三角形の内心について知っておきたい知識まとめ 理系ラボ



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




高校数学a 外角の二等分線と比 練習編 映像授業のtry It トライイット




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




角の二等分線の性質 線分比の公式 に関する定理の証明 理系ラボ
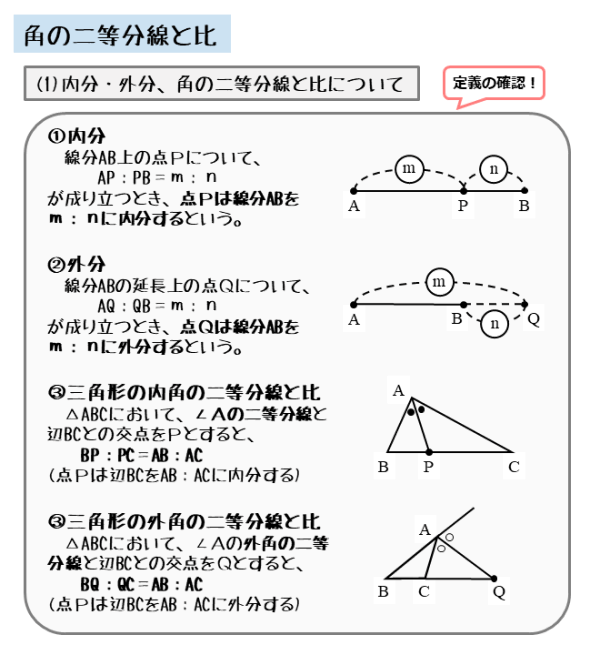



図形の性質 角の二等分線と比について 日々是鍛錬 ひびこれたんれん



Q Tbn And9gcrd P2pctuz8gfkpppw9apzd Qqafrxhfweennrb5u0gatejnzy Usqp Cau




高校数学a 外角の二等分線と比 練習編 映像授業のtry It トライイット
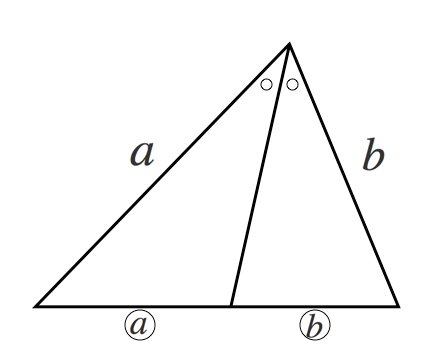



相似な図形 角の二等分があったらこれ 苦手な数学を簡単に



角の二等分線に関する重要な3つの公式 高校数学の美しい物語
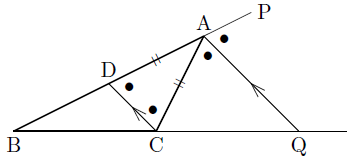



外角の2等分線と線分の比 まなびの学園




角の2等分線の性質を用いた長さおよび比を求める問題について 人力検索はてな




三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア



算数 基本 角の二等分線の性質 まいにち一題 中学受験過去問題研究




三角形の面積 応用 角の二等分線 Youtube
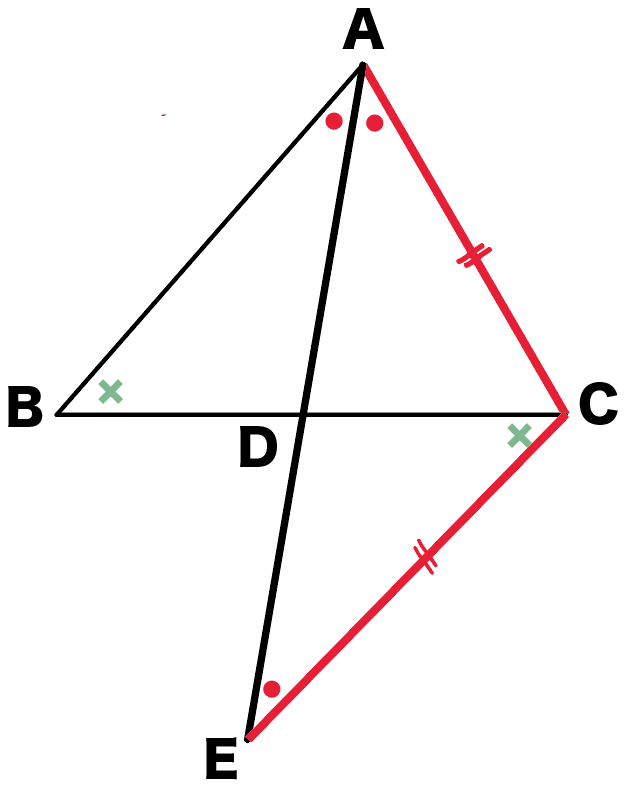



三角形の角の二等分線の性質 定理の証明がわかる5ステップ Qikeru 学びを楽しくわかりやすく



Q Tbn And9gcqnpctx1f6ittifhgiytdwhrngqknvekiryfqdwvgu6xpp5zoid Usqp Cau




角の2等分線によって分ける比 身勝手な主張



内角の二等分線と外角の二等分線の定理の覚え方と使い方




角の二等分線に関する問題 一目瞭然早見チャート 高校生 数学のノート Clear




角の二等分線の性質 線分比の公式 に関する定理の証明 理系ラボ



内角の二等分線と外角の二等分線の定理の覚え方と使い方



図形の性質 角の二等分線と比について 日々是鍛錬 ひびこれたんれん



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



三角形の外角の二等分線と比 Youtube



角の二等分線と辺の比 の証明 問題の解き方 数学fun




高校数学 数 98 三角形の内角の二等分線 Youtube
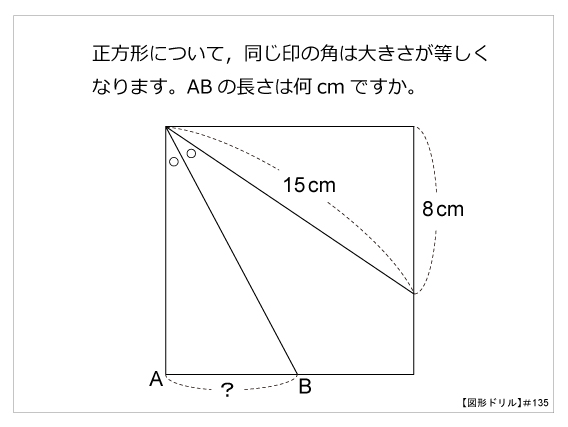



図形ドリル 第135問 角の2等分線 算数星人のweb問題集 中学受験算数の問題に挑戦



内角の二等分線と外角の二等分線の定理の覚え方と使い方



三角形の角の二等分線と比



角の二等分線
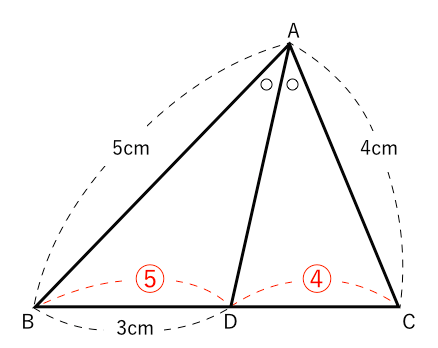



相似な図形 角の二等分があったらこれ 苦手な数学を簡単に




3数 角の二等分線と辺の比 Youtube




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
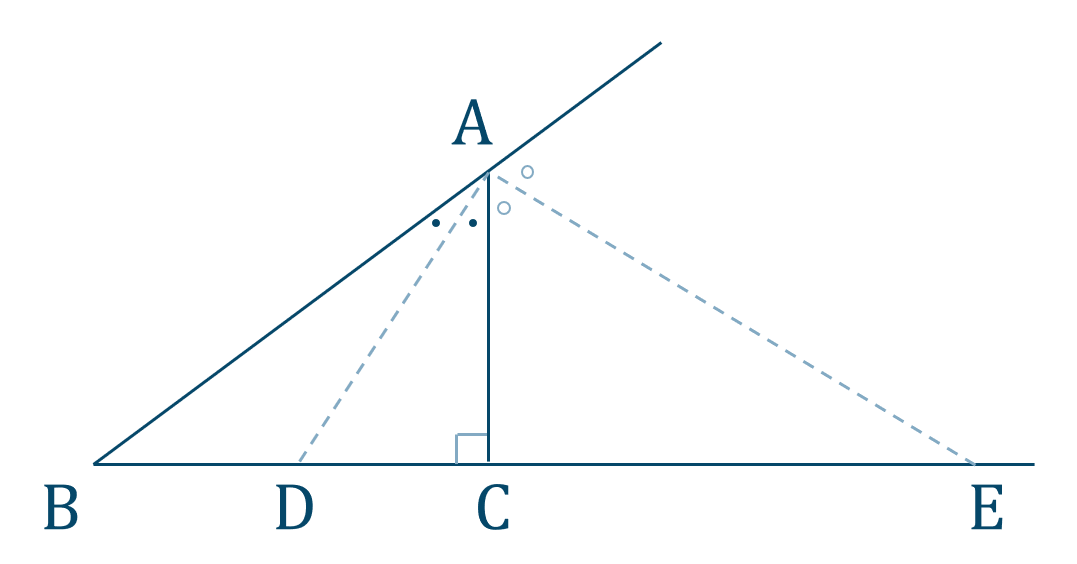



数学a 角の二等分線と比の使い方とコツ 教科書より詳しい高校数学



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学
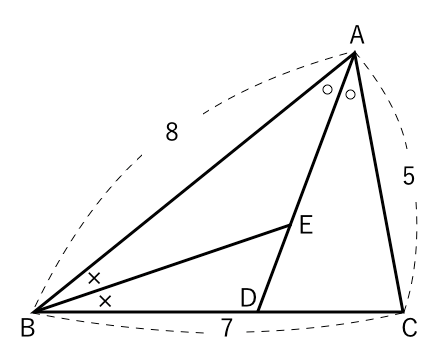



相似な図形 角の二等分があったらこれ 苦手な数学を簡単に




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




角の2等分線によって分ける比 身勝手な主張



中3数学 角の二等分線定理のポイントと練習問題
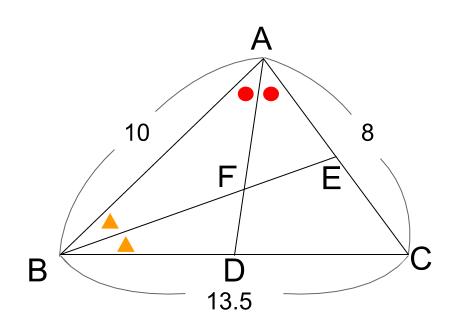



角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典



三角形の角の二等分線定理 外角




角の二等分線が図で誰でも一発でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




中3数学 相似な図形 Abcに二等分線をひいたとき Ab Ac Dc の証明 Youtube
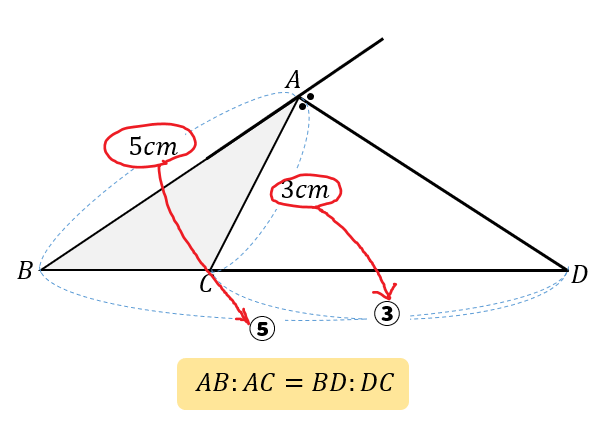



サクッと解説 角の二等分線と比の特徴となぜ について 数スタ



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学
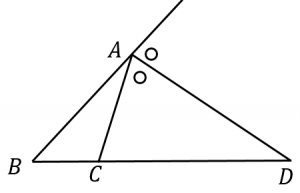



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学



中学3年生の相似な図形 角の二等分線と比に関する問題です 以下の写真 Yahoo 知恵袋
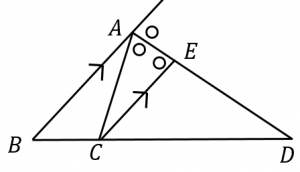



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
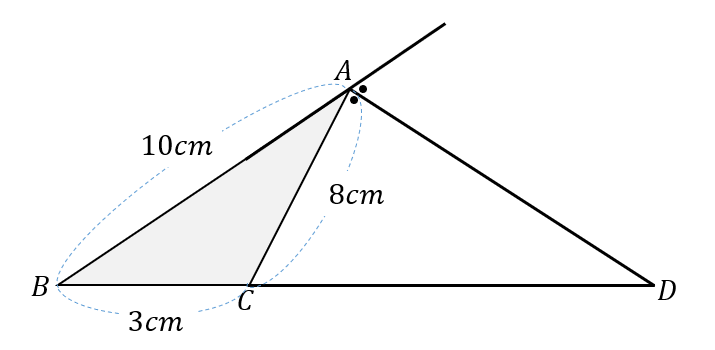



サクッと解説 角の二等分線と比の特徴となぜ について 数スタ


