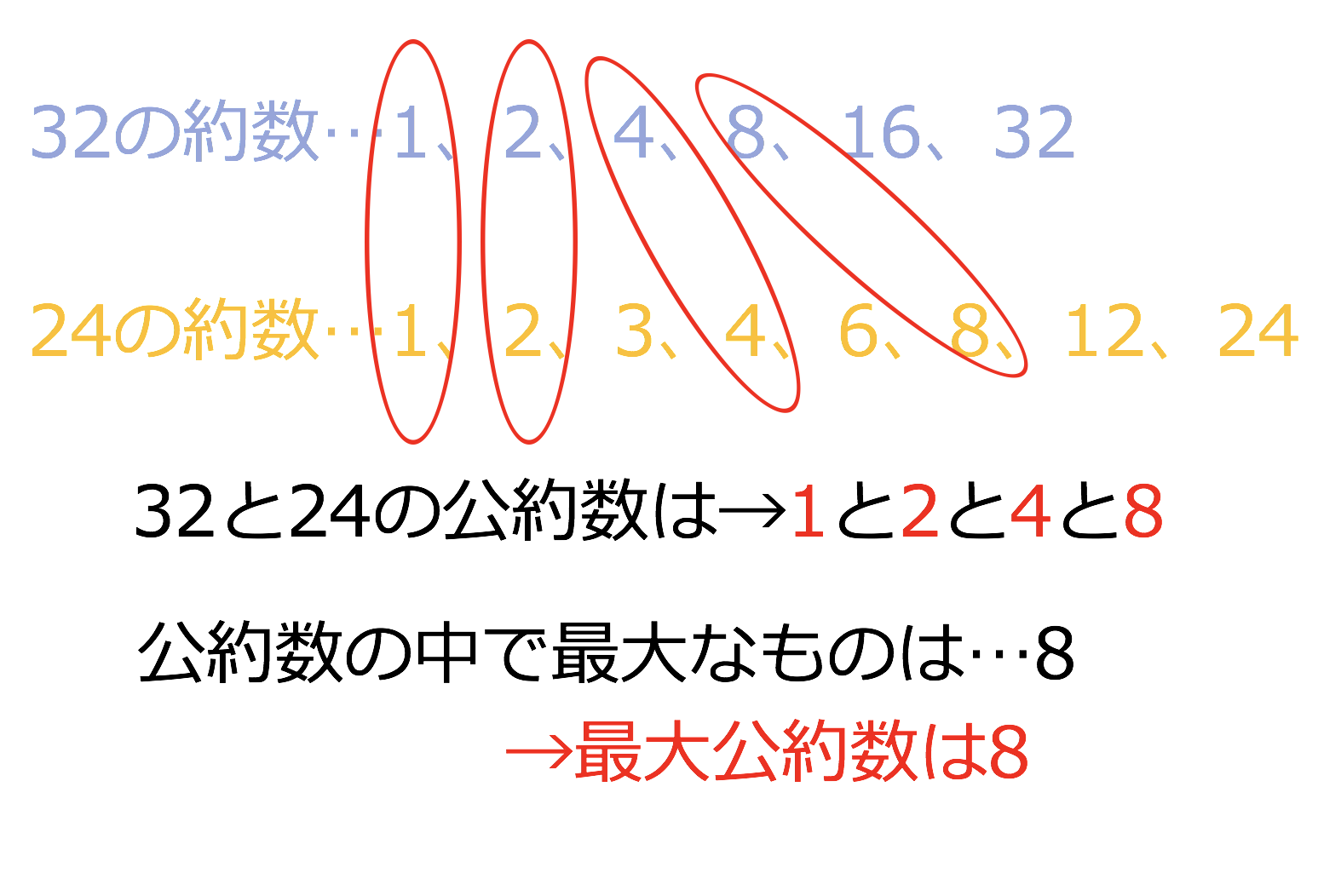
2つ以上の正の整数に共通な約数(公約数)のうち最大のものを 最大公約数 といいます. 例 12 と 18 の公約数は, 1,2,3, 6 で, 6 が最大公約数 2つ以上の正の整数の共通な倍数(公倍数)のうち最小のものを 最小公倍数 といいます. 例 2 と 3 の公倍数は, 6 ,12,18,24, で, 6 が最小公倍数 ※ 最小公約数 という言葉は使う値打ちがありません.なぜなら,公約数の 公約数・最大公約数の意味と求め方を学ぶ前に、まずは「約数」の理解が必要不可欠です。 約数についての基礎があやふやな場合は、まずは下記の記事をご覧下さい。 約数の意味と求め方 約数の簡単な求め方 約数の意味にプラスして、公約数・最大公約数の意味と地道な求め方も身につけましょう。 その方が 公約数・最大公約数に対する理解が深まり次の数の公約数の問題を解いてください。 公約数の求め方は、それぞれの数の約数を導き出した後に共通の約数を探します。 問1. 10と 問2. 9と18 問3. 15と35 問4. 12と24 問5. 52と64 問6. 4と12と36 問7. 15と30と45 スポンサーリンク 答え 答1. 10の約数:1、2、5、10 の約数:1、2、4、5、10

小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生
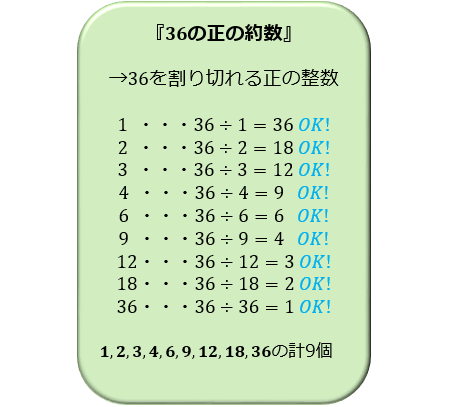
約数 公約数
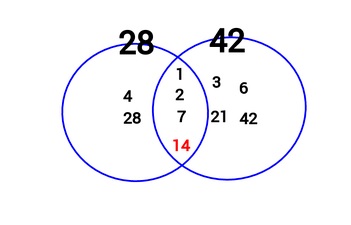
約数 公約数- 正の整数の約数の総和を表す公式を2つ紹介します。 1つ目は入試でも頻出の必須公式です。 2つ目はコサインが出てくる観賞用の公式です。玄人向け。 なお,約数の個数に関しては約数の個数の公式と平方数の性質を参照して下さい。 公約数は最大公約数の約数 まず、最も大事な性質が、「公約数は、最大公約数の約数」ということです。 もう一度28と42の例を見て確かめてみましょう。 図から28と42の公約数は1,2,7,14です。 また、最大公約数である14の約数も1,2,7,14です。



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ
最大公約数レベル3 算数問題集 約数問題集 6年生の算数 算数計算PDFドリルの算願 リンク:★漢字ドリル★教員様ライセンス★Kindle日替わりセールより、Pは28と14の最大公約数である14の約数です。 14の約数は、1,2、7、14の4個。 ただし、1で割ってあまりがでることはないので、 P=2,7,14となります。 求める総和は2+7+14= 23 となります。 参考 条件成立を自身の手で一度は確かめておきましょう。 2で割ったときのあまりはすべて1約数・公約数 計算機 3つのフォームに自然数を入力すると3つの数の公約数、 2つのフォームに自然数を入力すると2つの数の公約数、 どれか1つのフォームにのみ自然数を入力数するとその約数を求めま
よく見られている電卓ページ 因数分解の電卓 入力された式を因数分解できる電卓です。解き方がいくつもある因数分解ですが、この電卓を使えば簡単に因数分解がおこなえます。 連立方程式の電卓 2つの方程式を約数と公約数 1:このソフトの機能とねらい 任意の長方形を正方形ですきまなく敷きつめることを通して,公約数を理解させるシミュレー ション ・任意の大きさの長方形を設定しながら,敷きつめのできる正方形を選択することができる。 ・敷きつめが可能かどうかを一度に判断するのでは 最大公約数 まずは 16 と 56 の約数を求めてみよう。 16 の約数: 1、2、4、8、16 56 の約数: 1、2、4、7、8、14、28、56 二つの数の約数が全部出てきました。共通する約数は 1, 2, 4, 8 です。よって最大公約数は 8 となります。 16 と 56 の最小公倍数 16 と 56 の最小公倍数は 16 × 56 ÷ 8 = 112 となり
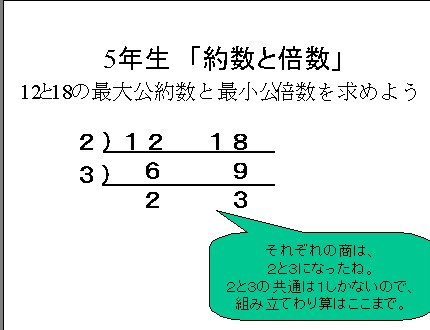
公約数、最大公約数、連除法 公約数と最大公約数を求めるには連除法を使えばいいです。 ルート記号をピンホールカメラで見ると連除法のアレになります。時々マジでどうでもいいことを差し込んでいきますよ。 さて、連除法をやってみましょう。48と72の公約数と最大公約数を求めます。AmazonでMaccessの約数・公約数―数の性質2 (思考力算数練習張シリーズ 36)。アマゾンならポイント還元本が多数。Maccess作品ほか、お急ぎ便対象商品は当日お届けも可能。また約数・公約数―数の性質2 (思考力算数練習張シリーズ 36)もアマゾン配送商品なら通常配送無料。公約数と最大公約数 公約数2つ以上の整数に共通な約数。 12の約数1、2、3、4、6、12 18の約数1、2、3、6、9、18 12と18の公約数は1、2、3、6 最大公約数公約数の中で最大な整数。 12と18の最大公約数は6。



算数4年から6年




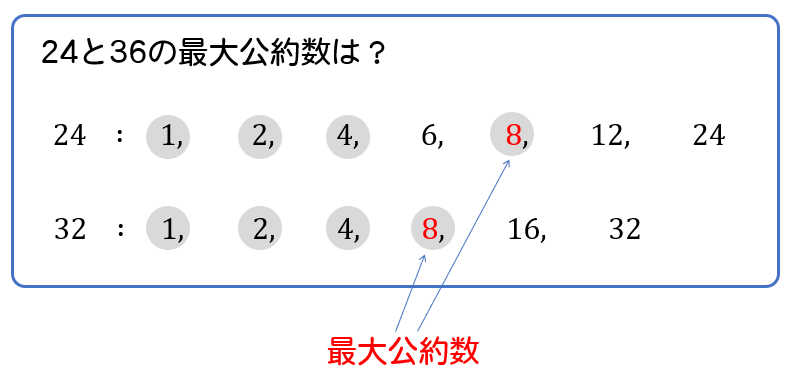
24と36の公約数と最大公約数 最小公倍数 Irohabook
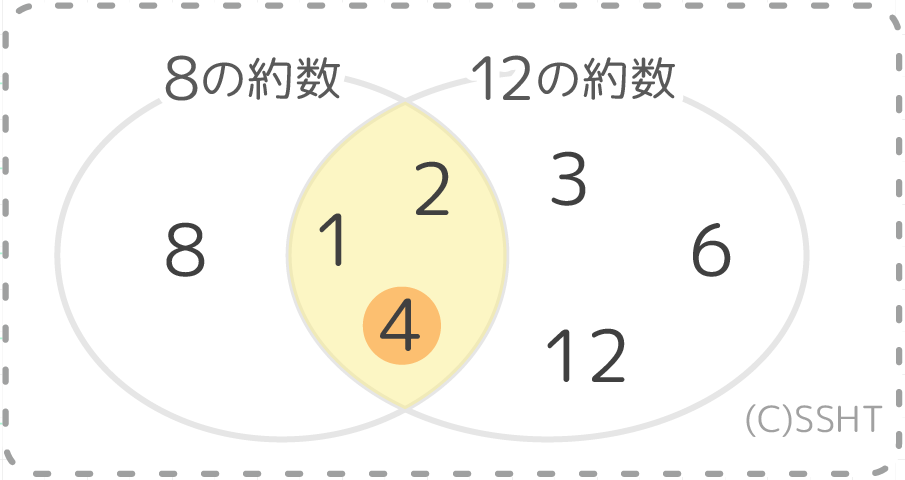
最大公約数 2つ以上の整数について、共通する約数をこれらの 公約数 といい、公約数のうち最大のものを 最大公約数 といいます。 公約数は最大公約数の約数になっています。 以下の例では、公約数 \(1,2,34,8\) はすべて最大公約数 \(8\) の約数になっていますね。 最大公約数とは|約数、公約数の意味も解説 最大公約数とは 公約数のうちで、絶対値が1番大きい数字。 最大公約数とは、公約数の中で1番大きい数字のことです。 例えば、 12 12 と 18 18 の最大公約数を求めてみましょう。 12 12 と 18 18 の約数はそれぞれ 12の約数 1,2,3,4,6,12 18の約数 1,2,3,6,9,18 12 の 約 数 1, 2, 3, 4, 6, 12 18 の 約 数 1, 2, 3, 6, 9, 18 です。 12 12 と精選版 日本国語大辞典 公約数の用語解説 〘名〙① 数学で、二つ以上の整数に共通な約数。最大のものを最大公約数という。整式に対しても準用する。公因数。〔数学ニ用ヰル辞ノ英和対訳字書(18)〕② 比喩的に、二つ以上のものが共通して有している要素。



3




C 最大公約数 最小公倍数を求める はなちるのマイノート
入力した自然数の約数を求めるサンプルプログラムを紹介します。 約数とは 約数とは、その数を割ることができる(余りがゼロ)数のことです。 例えば、「4」は「1, 2, 4」で割ることができるの、「1, 2, 4」は「4」の約数になります。 他の例もみてみましょう。 「8」の約数は「1, 2, 4, 8」です 約数と倍数② 公約数と公倍数とは 「公」という字は、「みんなの」とか「共通の」という意味です。 「公約数」の意味は、2つ以上の数の「共通の」約数ということ。 2つの数のファミリーの両方にいるメンバー(約数)ということですね。「2 約数と公約数」では,約数の意味,公約数と最大公約数の意味・求め方,適用問題 という流れになっている。公約数についても,日常生活の問題を扱いながら,倍数と対比さ せ,公約数の有限性に気付かせたい。また,約数が2個の数として素数を紹介する。 「3 偶数と奇数」では,偶数と




小5 算数 小5 約数 公約数 最大公約数 Youtube




約数 したがって 30と105の公約数は 1 3 5 15 性質2 約数 公約数 公約数の利用
算数の公約数とは まずは公約数の意味や公倍数との違いから見ていきましょう。 そもそも約数とは 約数とはある数をやり切ることができる整数(主に自然数)を指しますが、これは その数を掛け算で表した時に登場する数 のことです。 例えば、18を自然数同士の掛け算で表すと以下の3 公約数を考えよう! 公約数とは、共通の約数のことです。 上記の約数が解れば楽勝です。 例えば、10と12の公約数を考えてみましょう。 10の約数は、1、2、5、10 12の約数は、1、2、3、4、6、12となります。 共通の数字を探すと・・・ 10の約数は、 1 、 2 、5、10入力された値の約数を計算します。 約数を計算したい値を入力し「約数を計算」ボタンをクリックすると、入力された値の約数といくつ約数があるかを表示します。 (1~) 60の約数を求める 1, 2, 3, 4, 5, 6, 10, 12, 15, , 30, 60 約数の数:12個 約数・倍数の計算 ・素因数分解 ・最大公約数(2つの数)




最大公約数とは Youtube




分数を使いこなそう すだれ算って知ってる 前編 桜花 現役バイト塾講師 Note
約数と公約数 ③ なまえ 小年生 算数 プリント 計算プリントcom(keipricom) 公約数とは、2つ以上の整数の共通な 約数 ①(12、18)の最大公約数 中学数学 数と式 検索用コード 次の各組の数の最大公約数を求め,\ さらに公約数をすべて求めよ 公約数と最大公約数} {いくつかの整数に共通する約数}公約数のうち最大のもの {公約数と最大公約数の関係 {すべての公約数は最大公約数の約数 共通 a,bの任意の公約数は最大公約数の約数である $a,b$の任意の公約数を$d$, 最大公約数を$G$とするとき $lcm(d,G) = G$ が成り立つことを示す. $d,G$の最小公倍数を$l$とすると $lcm(d,G) = l$ 公倍数の定義より$G≦l$




大きな数の最大公約数の求め方 Youtube



1
この記事で公約数列挙の仕方が2つあることを学んだのでメモ qiitacom 公約数の列挙は 二つの整数を割り切れる数をループで探す 最大公約数の約数を列挙する の2通りあるらしい。 これをPythonで実装してみる。 目次 目次 1二つの整数を割り切れる数をループで探す 2最大公約数の約数を 約数と公約数「約数の個数が奇数⇔平方数」 14 ワンセンテンス算数 年12月16日 2248 フォローしました (記号「⇔」は同値という意味です。 約数の個数が奇数ならば平方数(整数の二乗)であり、平方数ならば約数の個数が奇数ということです小学校5年生 小五算数 小5算数 倍数と約数 約数と公約数学校図書
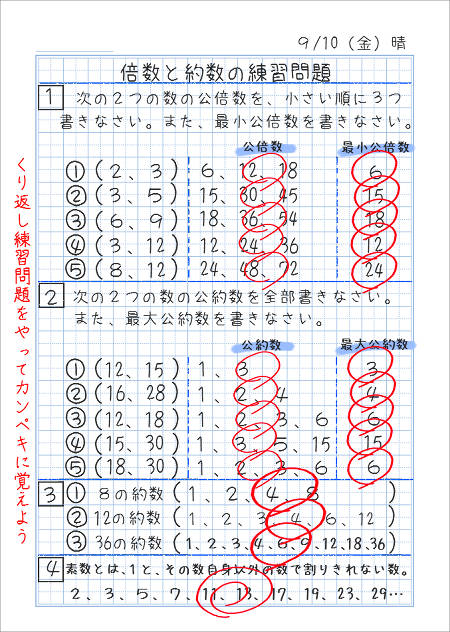



公約数と公倍数の自主学習ノート例 家庭学習レシピ
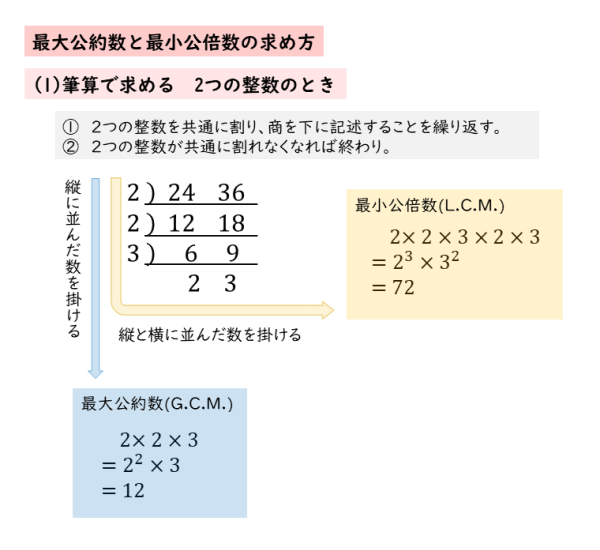



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん
公約数と最大公約数の意味を理解し、約数を漏れなく見つける能力が身についていれば間違えることはないでしょう。 ちなみに約数を漏れなく見つける方法についてはこちらにまとめています。 約数を漏れなく簡単に見つける方法|小学生でも素因数分解ができると便利! 小学校算数では




24と32の最大公約数と最小公倍数 Irohabook




公倍数や最小公倍数は公約数 最大公約数と似ていますが これらよりも若干難易度が上がり 考え方が難しくなります 公約数の 最小公倍数 小学校 算数 最大公約数




第回 数の性質 約数と倍数 分数 6年生 日能研の歩き方



約数の意味と約数の調べ方や簡単な求め方 まぜこぜ情報局




Lcm最小公倍数 Gcf最大公約数の英語表現を覚えよう ゆう アメリカ生活終了 英語勉強



5年算数整数 教え方のポイント



ドリルズ 小学5年生 算数 の無料学習プリント公約数 約分




約数 公約数 最大公約数 算数の教え上手 学びの場 Com



最大公約数とは 意味や簡単な求め方 計算問題 受験辞典




整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ



約数 倍数



数の性質 2 約数 公約数 Donnerlaketri Com



Fdk3a7ctb5192box5b Com Es 5nen Mt Yakusu Html



最大公約数とは 意味や簡単な求め方 計算問題 受験辞典




倍数と約数 最大公約数を求める 練習問題 Youtube



3



約数 公約数 最大公約数 約分 分数のたし算ひき算の授業 教材 算数5年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材
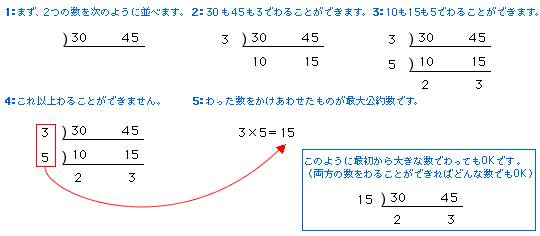



約数 公約数 最大公約数 算数の教え上手 学びの場 Com




約数 したがって 30と105の公約数は 1 3 5 15 性質2 約数 公約数 公約数の利用
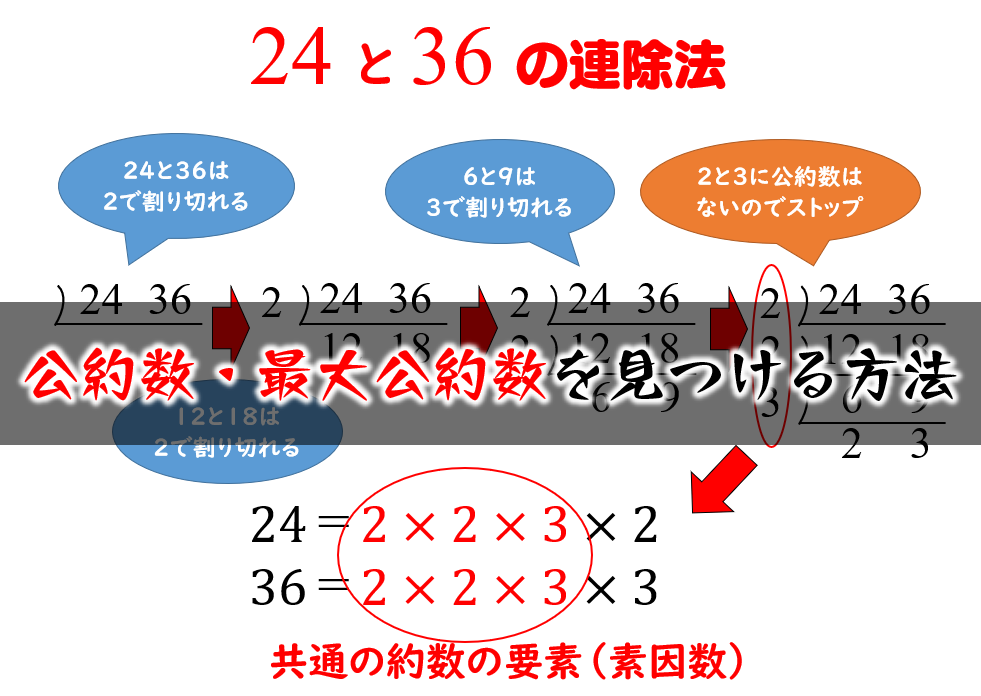



公約数 最大公約数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun



5年 公約数とベン図 のソフト 横山験也のちょっと一休み
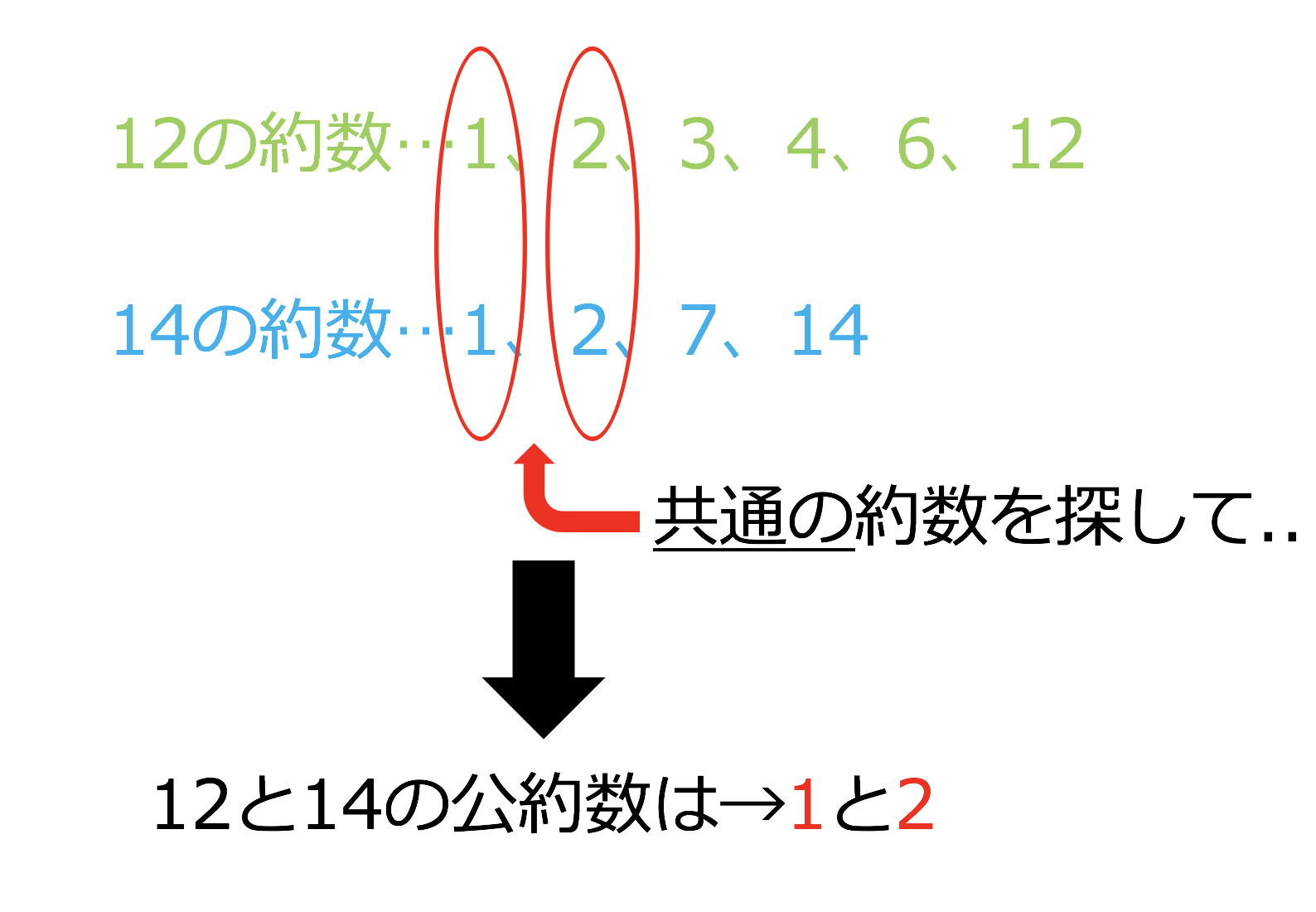



3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ
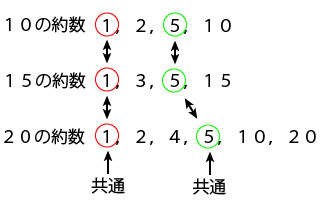



公約数の求め方 もう一度やり直しの算数 数学



約数 公約数 最大公約数 約分 分数のたし算ひき算の授業 教材 算数5年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材
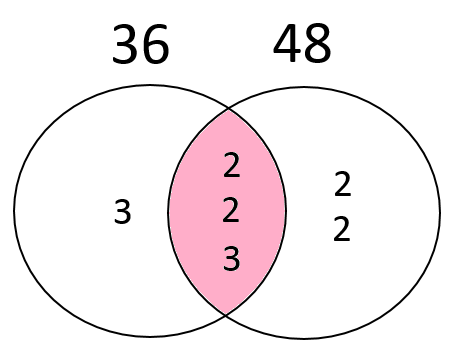



小学算数 最大公約数と最小公倍数を図を使って理解する 偏差値40プログラマー
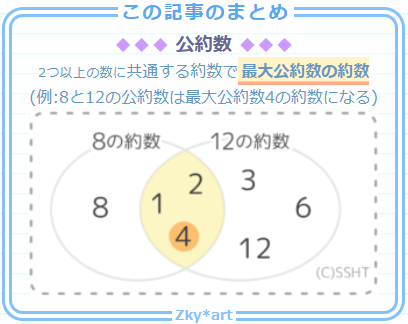



倍数約数 公倍数公約数 そうちゃ式 分かりやすい図解算数 別館




5年算数 整数の性質 公倍数 公約数 の簡単な求め方 マドリト フリーランスデザイナーのブログ




素因数分解 約数の個数と総和 公約数と公倍数




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ



1




9 12 Descubre Como Resolverlo En Qanda




学習プリント Com 約数 公約数 最大公約数の練習問題 約数 公約数 最大公約数でプリントが分かれているため お子さんの苦手箇所を選んで集中的に学習できます 倍数 公倍数 最小公倍数シリーズもあります 学習プリント 小学生 算数 約



最大公約数の意味と求め方 約数がいくつあるか簡単に調べる方法とは アタリマエ




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




小学5年生 算数 8月 約数と公約数 公倍数 公約数の利用 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ



最大公約数の意味と求め方 センター試験で使える解法を紹介 Studyplus スタディプラス



最大公約数の求め方 大人の学び直し算数 計算のやり方解説 無料




倍数 最小公倍数 約数 最大公約数 難しいな 7月 19年 泉小学校 ブログ 泉小学校




Lcm最小公倍数 Gcf最大公約数の英語表現を覚えよう ゆう アメリカ生活終了 英語勉強



算数でプログラミング教育 スクラッチで最大公約数を求めよう




公約数と公倍数の自主学習ノート例 家庭学習レシピ




倍数と約数 小5 公倍数 公約数 手探るは最強の解き方 算数の教え方教えますmother S Math Happy Study Support




約数の意味と求め方



48s96ub7b0z5f Net Yukuriddo Gojoho Kihon




小学5年生の算数 動画 約数と公約数の問題 最大公約数 19ch




1 約数と公約数 塾教材の販売 塾の 12と18の最大公約数 6 Pdf Document




中学受験 約数の個数の求め方は 素因数分解を活用すれば簡単です そうちゃ式 受験算数 新1号館 数論 特殊算
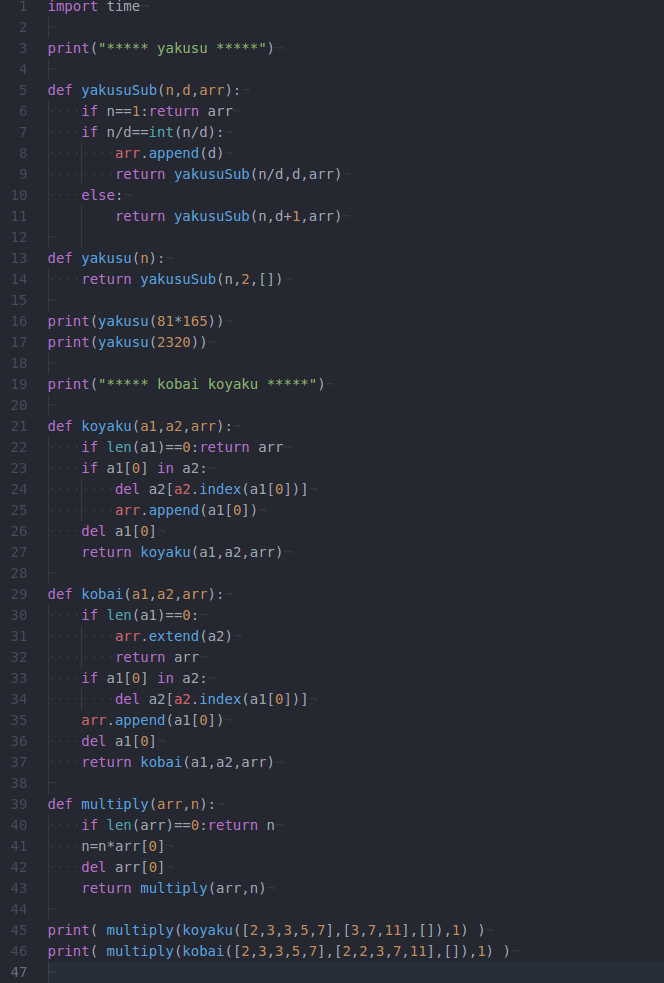



38 再帰 Pythonで約数を求める パーソナルブログメモリ




最大公約数 Wikipedia




Nitter




2講 最大公約数 最小公倍数 1節 約数と倍数 問題集 3章 整数の性質



Fdk3a7ctb5192box5b Com Es 5nen Mt Yakusu Html




28と63の最大公約数と最小公倍数を求めなさい という問題で答えが 最大公約数 Clear




最大公約数と最小公倍数の求め方とは ヒント 素因数分解 遊ぶ数学




倍数と約数 公約数と最大公約数 Youtube
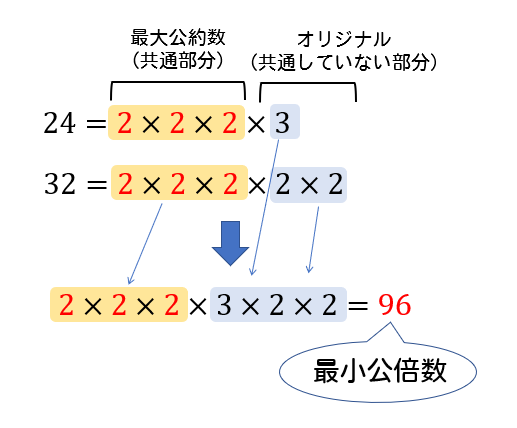



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ
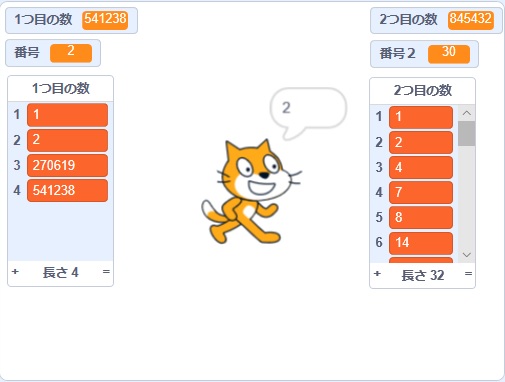



算数でプログラミング教育 スクラッチで最大公約数を求めよう




Kelas 7 Catatan Tentang 小学校の復習 最小公倍数 約数 Clear



72 48の公約数すべてを教えてください 約数の出し方 Yahoo 知恵袋



3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ



最大公約数の意味と求め方 約数がいくつあるか簡単に調べる方法とは アタリマエ
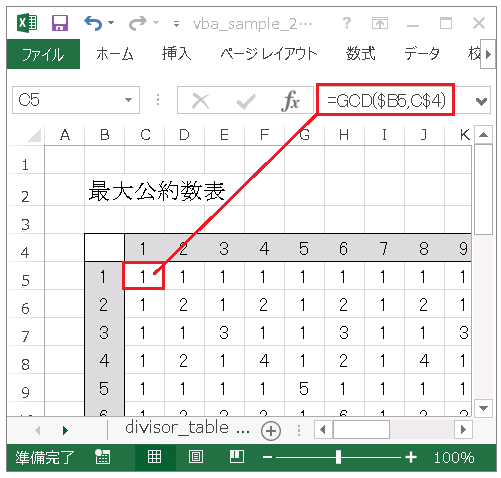



約数表と最大公約数表
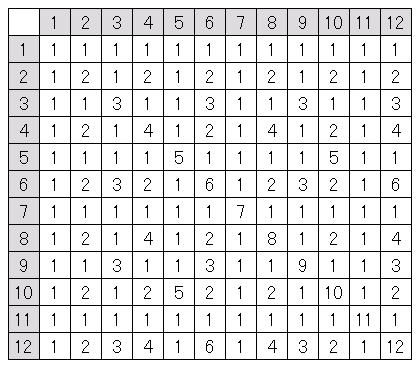



約数表と最大公約数表
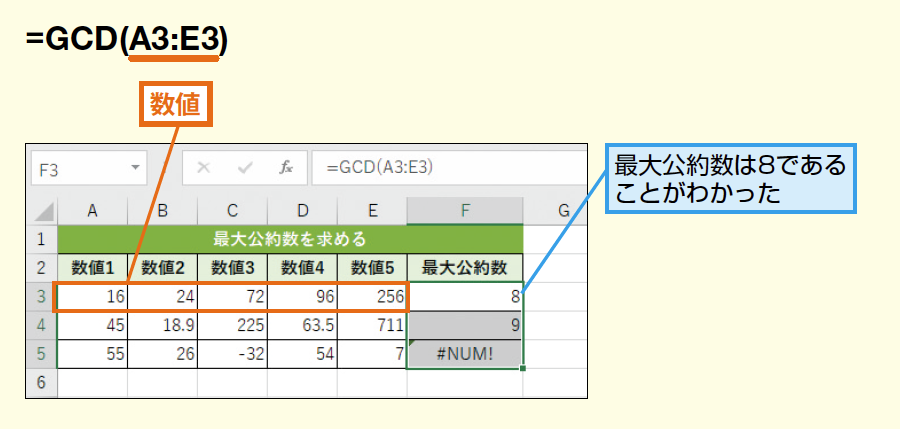



Gcd関数で最大公約数を求める Excel関数 できるネット




Square 12 18c Descubre Como Resolverlo En Qanda




高校数学a 最大公約数と最小公倍数の定義 受験の月




公約数 最大公約数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun



最大公約数の求め方 すだれ算 中学受験 塾なし の勉強




最小公倍数 最大公約数 小学5年生 計算無料プリント 小学生算数問題



小学5年生 約数 公約数の意味と求め方は 書き出し式 プリントあり そうちゃ式 分かりやすい図解算数 別館



公約数 最大公約数 最小公倍数を計算するページを作りました If1tech



Fdk3a7ctb5192box5b Com Es 5nen Mt Yakusu Html



最大公約数 最小公倍数




倍数 約数 算数用語集




最大公約数レベル1 問題 385 400




小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生




小5 算数 小5 19 約数と公約数 Youtube




中学数学3年 公約数と最大公約数 受験の月




倍数 最小公倍数と約数 最大公約数を教えてみた 妹z会中学受験コース4年




最大公約数と最小公倍数の暗記ドリル たぶお Sapix サピックス A1 養成講座




動画解説 みんなの算数オンライン 公約数 は 最大公約数の約数 超重要




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料
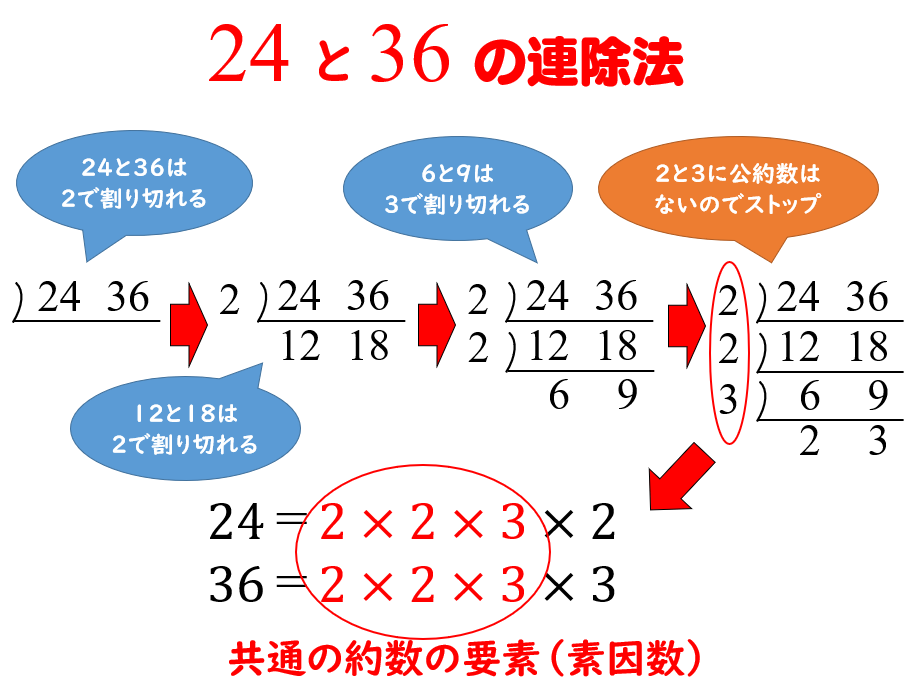



公約数 最大公約数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun



最小公倍数 最大公約数のドリル
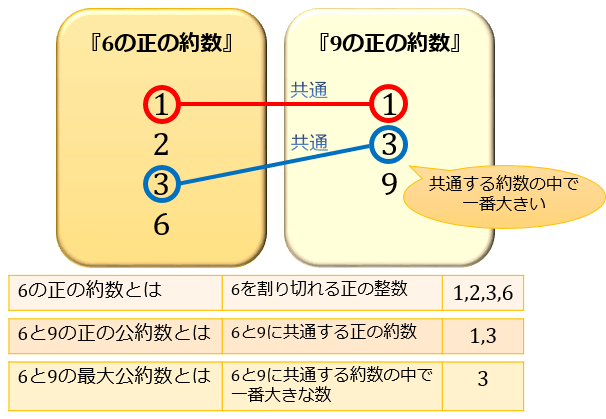



最大公約数の意味と求め方 約数がいくつあるか簡単に調べる方法とは アタリマエ
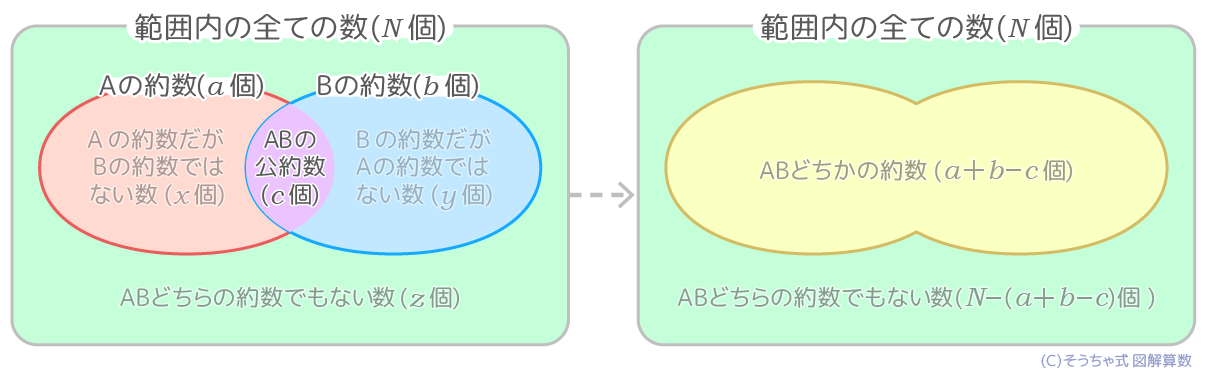



中学受験 公 倍数 公 約数の基礎から応用問題まで全部まとめ そうちゃ式 受験算数 新1号館 数論 特殊算




倍数と約数




公約数 公倍数の求め方 Z Square Z会




倍数 約数 算数用語集



最大公約数の求め方 大人の学び直し算数 計算のやり方解説 無料




公約数の求め方 もう一度やり直しの算数 数学


