今回は平方根の利用問題を見ていく。 特に詰まりやすいところなので、ゆっくりとやっていこう。 前回←平方根の計算(標~難) 次回→平方根の利用(2)整数部分小数部分(標~難) 24 平方根の利用 241 整数・自然数になるようにする(標~難) 242 整数部分,小数部分(標~難)整数の加法・減法・乗法 / 二次式の展開と因数分解 / 実数と平方根 / 一次不等式 / 二次方程式など 二次関数 三次式の展開と因数分解 / 二項定理 / 整式の割り算など 複素数と方程式 複素数 / 解と係数の関係 / 剰余の定理と因数定理 / 高次方程式 複素数の計算 / 解と係数の関係の利用 / � このように平方根の割り算は中身を計算してあげるだけでいいです。 整数÷平方根 一般的にはこのようになります。 整数=平方根の2乗 ということを利用するだけです。 具体例を見ていきましょう。 例 整数と平方根が同時に現れると戸惑うかもしれません。

平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく
平方根 割り算 整数
平方根 割り算 整数-数学において、無平方数 (むへいほうすう、英 squarefree integer )または平方因子を持たない整数 (integer without square factors) とは、平方因子を持たない数、すなわち 1 より大きい完全平方で割り切れないような整数(通例として正の整数)をいう。 与えられた整数が無平方数であるとき、そ平方根が整数となる条件 4パターンの例題 整数 平方根 (ルート)で表された式が整数となる条件を求める問題の解き方を紹介します。 かけ算、分数、足し算、引き算の4パターンを解説します。




中3数学 平方根の計算の仕方を極めよう 掛け算 割り算も 都立高校受験応援ブログ
午後のひとときに、平方根を連分数にしてみよう。 小学校の算数の話しから始めましょうか。 小学校に入ると、まずは自然数の足し算を習います。 続いて、自然数の引き算を習います。 すると、負という概念が現れます。 自然数にゼロと負の自然数合わせたものが整数です。 自然数の掛け算 ここでは、負の数の平方根について見ていきます。計算間違いをしやすい部分があるので、注意してみていきましょう。 マイナス1の平方根 すでに知っている $ sqrt{2}$ という数について考えてみましょう。これはどんな数字ルートを簡単にする 例題をといてみよう。 例題 つぎのルート分数の割り算をしなさい。 5分の√ ÷ √(15分の2) Step1 掛け算になおす
平方根の加減 3 +2 を例に それ以外で が正の整数 になる時を考えると = ×( × ) = ×( × ) = ×( × ) などのように に同じものを2回かけ合せたときがこれにあたる。 したがってa=5、、45 ☆ 勉強内容の解説・ガイド ☆ ☆ 教育ママ・教育パパ 応援宣言! 誰にでも家庭で簡単に次の平方根を、整数×平方根、または整数の形にしてみよう。 \(√45\) \(√56\) \(√121\) 答え 次の整数を素因数分解しよう。 \(2×3×5\) 解説\(30\)を\(2\)で割ると\(15\)、\(15\)を\(3\)で割ると\(5\)となることから、\(30\)は\(2\)と\(3\)と\(5\)の積で表されることが分かる。 これで整数部分が平方根の記号が付いた値の整数部分が求まりました。 つまり、小数部分は \(\sqrt{16}44\) ということになります。 ここからは、この平方根の小数部分についての計算式を、工夫して解く方法をご紹介します。
整数と平方根は別々に掛け算・割り算をする ただ重要なのは、 整数と平方根を分けて掛け算または割り算をすることです。 整数と平方根はまったく別の数字だからです。 ルートでは 3 2 などの記載されることがあります。 これは3と 2 の掛け算であり、 3 × 2 と意味は同じです。 ただ × を省略するのが基本なので、 3 2 と記されます。 ルートの前にある数字 平方根に文字が含まれていて整数になるときの文字を求めるような問題です。 図形の問題で三平方の定理あたりと組み合わせられることもあるかもしれませんね。 夢を叶える塾 数学を通して夢を叶える力を育む米沢市の学習塾 フォローする 夢を叶える塾 簡単なご案内;割り算の場合には、そのまま計算しても約分などによって簡単に計算できることが多いです。 (5)の問題解説! 平方根 ルートを整数にするnの値の見つけ方!素因数分解の利用がポイント! 平方根 116 中3数学平方根、ルートの値を語呂合わせ!覚え方まとめ;




平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ




平方根の割り算 さわやか さくらぐみ
SRT割り算器を、多少改造すると平方根も計算できる。 (10の4乗)の平方根は100 (10の2乗)というように平方根をとると、指数の値は元の数の指数の半分になる。ただし、整数などで表せる平方根はルートを使わない形で表す。 大きい数の平方根は?3桁の数は暗記も必要! さぁ、ルートという記号を学んだことで 平方根は今度こそバッチリだぜ! と、いきたいところなんですが 121の平方根は? んーーっと ルートを使って \(\pm \sqrt{121}\)でしょ1.平方根のわりざんについて 平方根の割り算 を計算する時は、平方根の掛け算を計算する時と同じように、平方根の値どうしとそれ以外の値どうしを、普通に掛けたり割ったりできます。 平方根の掛け算の計算については、こちら かけざん(平方根の計算) を見てください。 したがって、平方根の足し算や引き算の計算のようにルートの中の値を合わせなくても




平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく
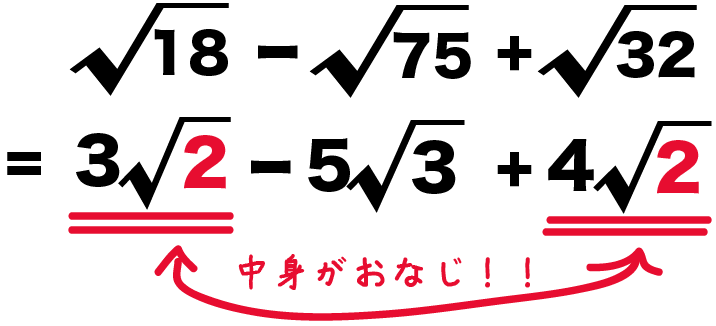



平方根 ルート の足し算 引き算の仕方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
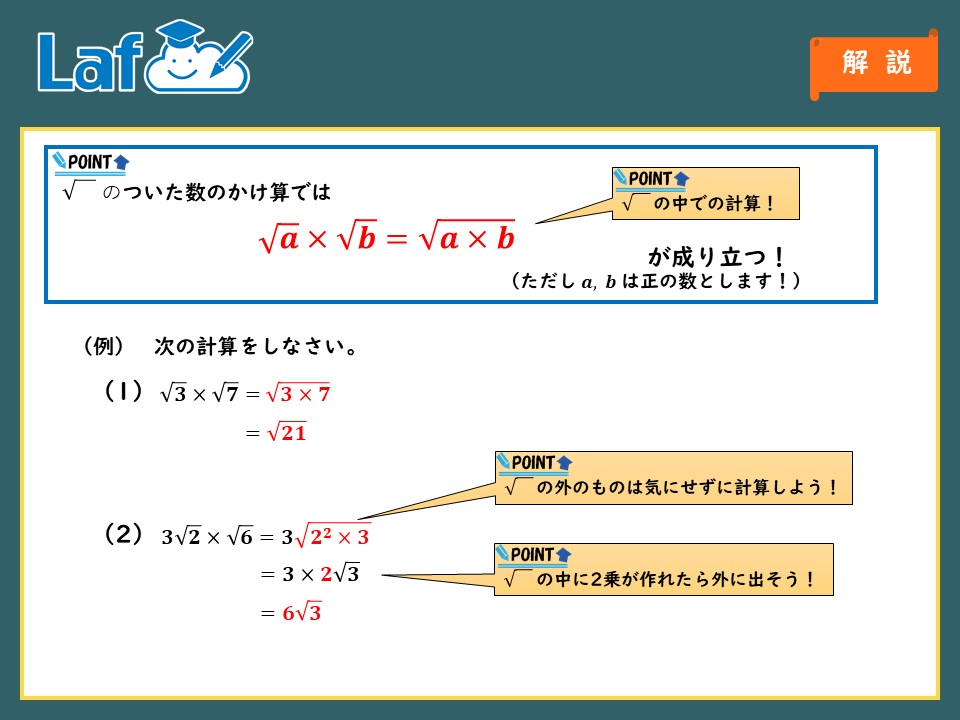
整数演算で平方根 17年1月9日 hira コメントする 最近、整数演算だけで色々する話があったので、過去に作成したものを見直してみた。 ・平方根 これは、ファミコン時代から使っていた方法をC++(C)で表現したもので。 ※アルゴリズムは 用高阶函数filter() 判断一个数的平方根是否是整数 今天学习Python的高阶函数: filter()函数是 Python 内置的一个高阶函数,filter()函数接收一个函数function 和一个列表list,这个接收到的函数function的作用是对列表list中每个元素进行判断,返回 True或 False,filter()根据判断结果自动过滤掉不符合条件(False③平方根のかけ算・割り算 平方根のかけ算と割り算は、 ルートの中身をそのままかけ算・割り算します。 \(5\sqrt{2}×3\sqrt{2}\) を計算してください
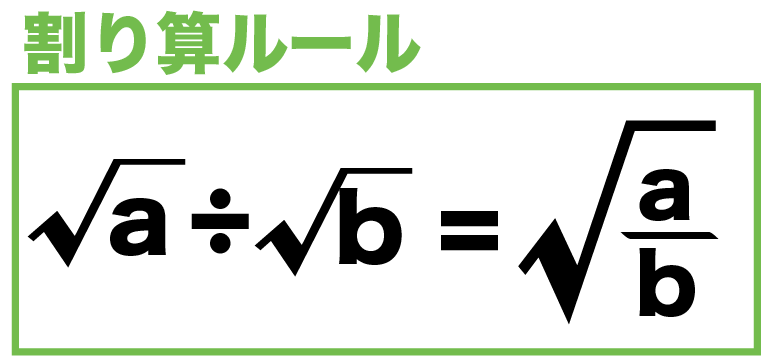



平方根 ルート の割り算の計算方法の5つのステップ Qikeru 学びを楽しくわかりやすく



高校入試の平方根をたった3分で 得意 にする方法 高校入試徹底対策ガイド
よって、平方根を求めようとする数値から平方根の値を持つ整数の個数の値、3,5,7,9,・・・を順番に引いていき、0以下になった回数が求める平方根の値となります。 具体的な数値で確かめてみましょう。例えば19の場合、1回目の計算 193=16、2回目の計算 165=9、3回目の計算 97=2、4回目の計算 29 平方根をとった数字を一回文字列に変換します。 そして、''が何番目に存在するかを取得し、 ''の位置から2番目、つまり小数第2位に当たる数が存在するかどうかを判定し、 存在した場合は、整数でない、存在しない場合は、整数という風に判別しました。※平方数とはある整数の平方(2乗)になっている数のこと。4=2 2 や9=3 2 は平方数。 例題2 が自然数となる自然数nを求めなさい。 答案 根号が外れるためには,根号の中は,平方数になっていなければならない。 243n=3(8n) だから 根号の中が平方数になるには8n は3の倍数 8n=3,6 このうち根号



平方根の問題です 3 16の をはずしたいんですがやり方を忘れて Yahoo 知恵袋




平方根の掛け算 割り算 ルート計算と素因数分解のやり方 リョースケ大学
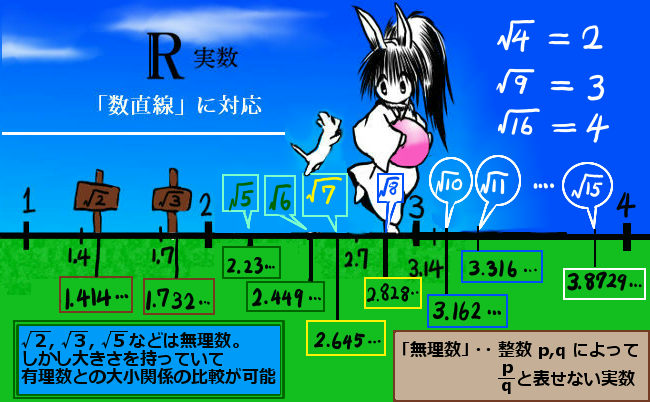
平方根 平方根とは、2乗する前の数のことです。例えば、 a^2=4 という関係を満たすとき、 a のことを4の平方根と言います。つまり、4の平方根は、2と ー 2 になります。 では、3の平方根は、何でしょうか。 a^2=3 を満たす a は、少なくとも整数ではなさそうです。平方根を整数で表せない平方根と無理数 ルートのついた無理数の代入にはちょっとしたコツがあります。 代入問題はずっと出てきますが、少し応用された問題で条件式の使い方のポイントを解説をします。 高校の数学でこれを知らずにいたらかなりの差がついてしまうので今のネイピアの骨には 九九 の表が組み込まれており、複数の桁からなる 正 の 整数 と、1桁の正の整数の 掛け算 の計算を 足し算 だけで済ますことができる。 その応用として、複数桁同士の掛け算や 割り算 、 平方根 を求める計算ができる。 ネイピアの骨は、枠を持つ 基盤 (図中では「BOARD」)と、乗算や除算を行うために基板上に配置される ネイピアの棒




中3数学 平方根の計算の仕方を極めよう 掛け算 割り算も 都立高校受験応援ブログ



1
平方根 √ 、立方根 3√ 、累乗根 n√ を計算します。2× √2 3× √2 = (2 3)× √2 = 5√2 2 × 2 3 × 2 = ( 2 3) × 2 = 5 2 また、 √2 2 や √3 3 などの平方根は整数で表せませんが、定数(決まった値)です。 小数にするとループせずに無限に続く数(無理数)なので π π と同じ種類の定数ですね。 なので 2π 3π = 5π 2 π 3 π = 5 π となるのと同じことなのです。 ルートの中が異なれば平方根は全く異なる定数となるので 整数の平方根を求めるとき、 素因数分解をしたのは、 平方根の中の数字を小さくするのが目的じゃったんじゃ トンちゃん そうですね! 数学おじさん 平方根の中に、2乗の部分があれば、平方根がとれる わけじゃ 以下の公式を使うわけじゃな 数学おじさん 平方根の中に2乗があるときの




平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学
初等整数論 import import sympy as sym 浮動小数の世界から整数の世界へ 整数のつもりで計算していたらいつの間にか浮動小数になっていた。 ありがちなバグである。 割り算、剰余算、天 分母の5で75は15に約分できる。 そこから有理化で分子分母に√5を掛けてさらに約分。 75×27/ (5√5) =15×27/√5 =15×27×√5/5 =81√5 ちなみに√5×√5=5 これは分かりますよね? 整数×平方根 まず、整数と平方根の掛け算からです。 一般的に となります。 例をいていきましょう。 例 以上です。 簡単ですね。 文字式と同じように×を省略して表記すればokです。 平方根×平方根 続いて、平方根同士の掛け算です。 一般的に となります。



平方根の掛け算は 1分でわかる意味 計算のやり方 公式 分数の掛け算




平方根の計算 ルート分数の割り算の仕方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




平方根の掛け算 割り算 ルート計算と素因数分解のやり方 リョースケ大学



3




整数をルートにする方法 5秒で計算できる簡単な問題だ 中学や高校の数学の計算問題




平方根の割り算 さわやか さくらぐみ




平方根 ルート の割り算の計算方法の5つのステップ Qikeru 学びを楽しくわかりやすく




平方根の足し算と引き算 ルート計算のやり方や分数の求め方 リョースケ大学




平方根の割り算 さわやか さくらぐみ




数学も英語も強くなる 意外な数学英語 Unexpected Math English Long Division



1




平方根分野の難所 掛け算と割り算をていねいに あんず学習塾のメモ 図表置き場




私はまず割り算を分数にして平方根は平方根で 整数は整数で約分したんですけど この方法 Clear




高校入試の平方根をたった3分で 得意 にする方法 高校入試徹底対策ガイド




私はまず割り算を分数にして平方根は平方根で 整数は整数で約分したんですけど この方法 Clear




平方根の掛け算 割り算 ルート計算と素因数分解のやり方 リョースケ大学
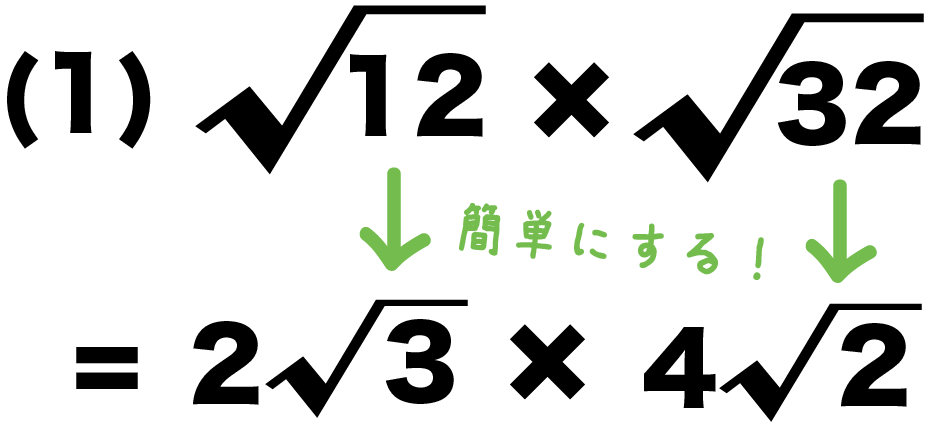



平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




平方根 ルート の割り算の計算方法の5つのステップ Qikeru 学びを楽しくわかりやすく




平方根の計算 ルート分数の割り算の仕方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




エレガント分数 掛け算 割り算 やり方 最高のカラーリングのアイデア




平方根 ルート の割り算の計算方法の5つのステップ Qikeru 学びを楽しくわかりやすく




R言語 Rstudioを使って計算 はじめての関数 Eiko Programming Note




平方根の掛け算 割り算 中学数学 平方根 5 Youtube



高校入試の平方根をたった3分で 得意 にする方法 高校入試徹底対策ガイド
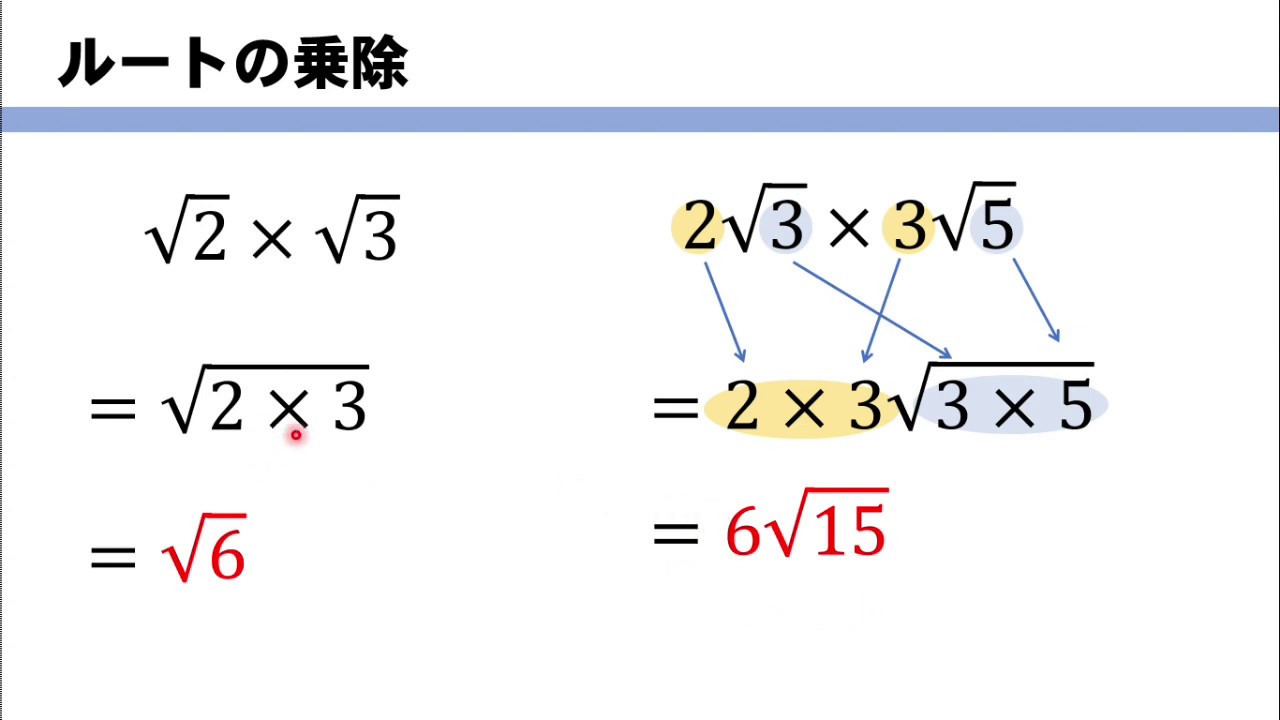



平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ
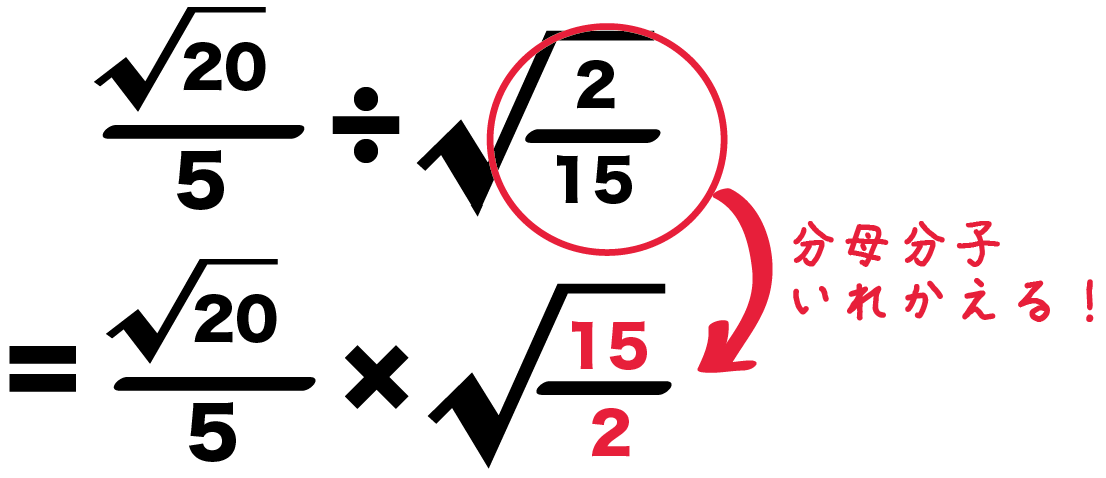



平方根の計算 ルート分数の割り算の仕方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




これで完璧 平方根の基礎 中3数学 中学生の勉強法



平方根の割り算は 1分でわかる計算 割り算の問題とやり方 有理化 分数との関係



Wcb5pawc3ujbkm



これで完璧 平方根の基礎 中3数学 中学生の勉強法




平方根 ルート の割り算の計算方法の5つのステップ Qikeru 学びを楽しくわかりやすく



平方根って何だろう 理数系無料オンライン学習 Kori




ルートの整数部分と小数部分 求め方はこれを覚えるだけ 中学や高校の数学の計算問題



平方根 ルート の割り算の計算方法の5つのステップ Qikeru 学びを楽しくわかりやすく



Q Tbn And9gcqrowgvqn H0mpsul5gslm5oso Kohgdb3kvug Q8m84kyw0il Usqp Cau
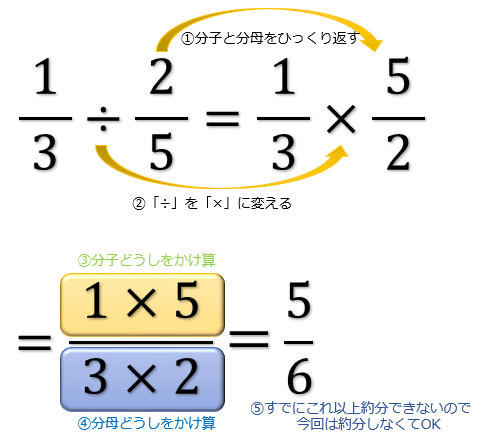



分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ




ルートの掛け算の問題 やり方は乗法とほとんど同じ 中学や高校の数学の計算問題



平方根の計算です なぜ分母が整数なのに有理化をするので Yahoo 知恵袋




平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ




平方根分野の難所 掛け算と割り算をていねいに あんず学習塾のメモ 図表置き場




平方根 ルート の重要な計算方法まとめ 数学fun




中3数学 平方根の計算の仕方を極めよう 掛け算 割り算も 都立高校受験応援ブログ




平方根の掛け算 割り算 ルート計算と素因数分解のやり方 リョースケ大学




ルートの四則演算 計算する順番に注意しよう 中学や高校の数学の計算問題



平方根とは 計算方法や求め方 近似値の覚え方 利用問題 受験辞典




ルートが整数になる数 チーム エン




平方根の足し算と引き算 ルート計算のやり方や分数の求め方 リョースケ大学




平方根の割り算 さわやか さくらぐみ




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




これで完璧 平方根の基礎 中3数学 中学生の勉強法




平方根の計算 ルート分数の割り算の仕方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
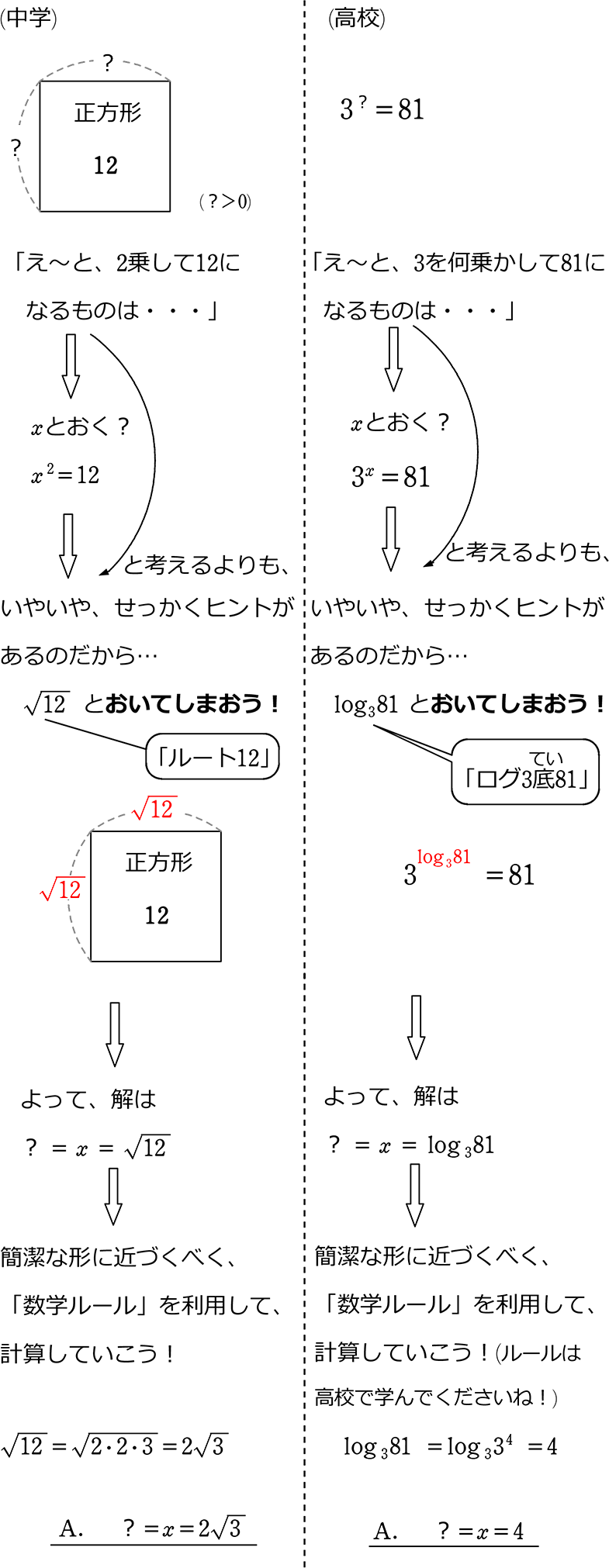



中学数学 平方根




平方根 ルート の重要な計算方法まとめ 数学fun




平方根の割り算 さわやか さくらぐみ




平方根 ルート の割り算の計算方法の5つのステップ Qikeru 学びを楽しくわかりやすく



この値が整数となる自然数nのうち 最小となるものを求めなさい という問題が分か Yahoo 知恵袋




ルートのかけ算と割り算 中3数学 Youtube




中3数学 平方根の計算の仕方を極めよう 掛け算 割り算も 都立高校受験応援ブログ




平方根の掛け算 割り算 ルート計算と素因数分解のやり方 リョースケ大学




平方根の除法 チーム エン




平方根 ルート の重要な計算方法まとめ 数学fun




平方根の問題の解き方 6パターン 数学fun




平方根 ルート の重要な計算方法まとめ 数学fun




平方根の割り算 さわやか さくらぐみ



整数 ルートのやり方は 1分でわかる計算 割り算 ルートの掛け算 足し算
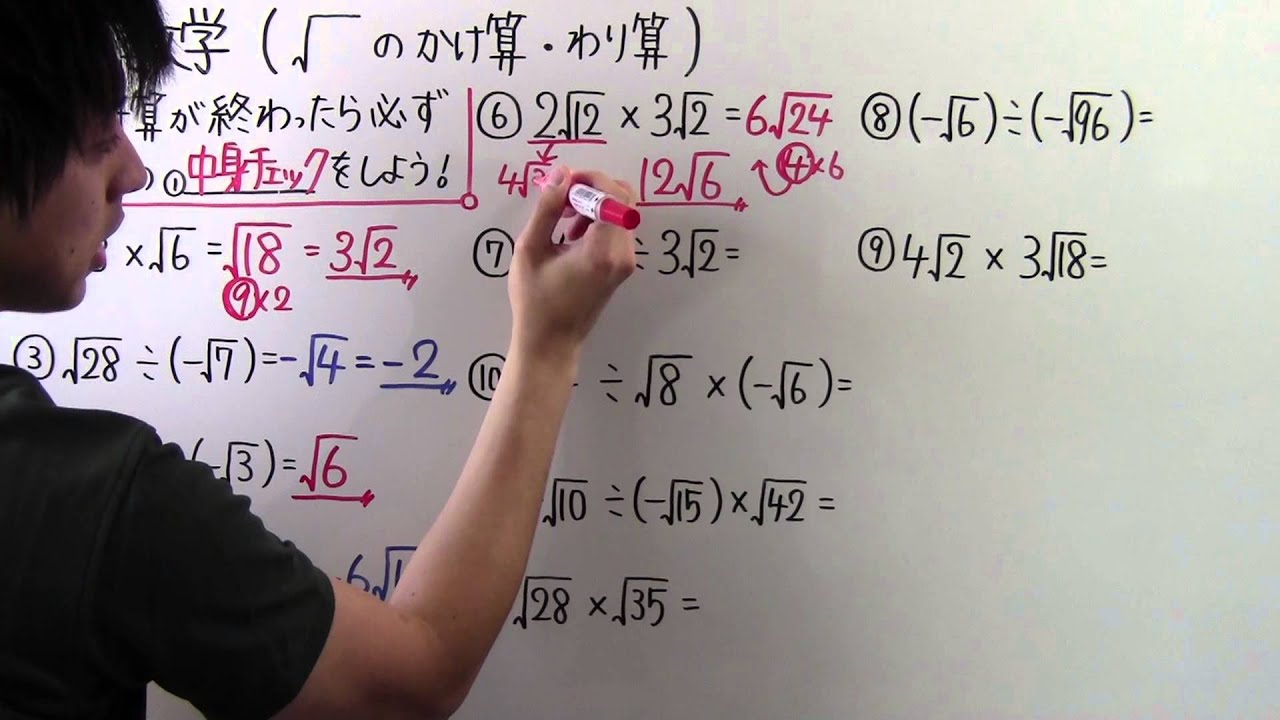



数学 中3 18 ルートのかけ算 わり算 Youtube



整数 ルートのやり方は 1分でわかる計算 割り算 ルートの掛け算 足し算




平方根の割り算 さわやか さくらぐみ




ルートの割り算の問題 やり方は を合体して中で割るだけだ 中学や高校の数学の計算問題




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




ルートの引き算 解き方は足し算の問題の時と全く同じで簡単だ 中学や高校の数学の計算問題



平方根の掛け算は 1分でわかる意味 計算のやり方 公式 分数の掛け算




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




中3数学 平方根の計算の仕方を極めよう 掛け算 割り算も 都立高校受験応援ブログ




平方根 ルート の割り算の計算方法の5つのステップ Qikeru 学びを楽しくわかりやすく




平方根の計算 ルート分数の割り算の仕方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




平方根の利用 1 整数 自然数になるようなn 標 難 数学の解説と練習問題



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




平方根の割り算 さわやか さくらぐみ




中3数学 平方根の計算の仕方を極めよう 掛け算 割り算も 都立高校受験応援ブログ




平方根分野の難所 掛け算と割り算をていねいに あんず学習塾のメモ 図表置き場




平方根の割り算 さわやか さくらぐみ




中学3年数学の問題です 整数をルートに入れる問題でよくわからないの 数学 教えて Goo




数学 中3 21 ルートの計算のまとめ Youtube




平方根 ルート の割り算の計算方法の5つのステップ Qikeru 学びを楽しくわかりやすく




ルート 平方根 の計算




平方根 ルート の重要な計算方法まとめ 数学fun



分数 整数 ルートの計算方法を教えてください下の画像の計算方法を教えて Yahoo 知恵袋




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




平方根の割り算 さわやか さくらぐみ




平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく


